DNA Melting: Simulating DNA Melting - Basics
Contents
Introduction
This tutorial will show you how to simulate the DNA melting experiment with Matlab. The DNA melting apparatus you will build produces two output voltages related to the sample temperature and fluorescence intensity. During an experimental run, these two voltages will be recorded periodically. At the end of this tutorial, you should be able to produce mock datasets that are similar to what you will record in the lab. You can use simulated datasets to help develop and debug your data analysis scripts.
It will be essential to have working data analysis scripts before you begin running experiments in the lab. When you have completed this tutorial, refer to the lab manual for data analysis instructions.
The procedure for creating the simulation is:
- Write a function to compute the equilibrium dsDNA contration vs. temperature
- Model sample temperature versus time during an experimental run
- Compute the RTD voltage from temperature vs. time data
- Add noise to the RTD signal
- Compute relative fluorescence intensity from temperature vs. time data
- Model photobleaching (optional)
- Scale the fluorescence intensity signal and add noise
- Reformat the data to match what is produced by the DNA melting software
You will not have to write any new code to complete this tutorial; however, you should open a Matlab window and follow along as you read. Code from this page can be copied and pasted into the Matlab command window. M-files are available in the course locker.
If you prefer to work in Python, please see this page.
Before you begin
- Read the Measuring DNA Melting Curves Lab Manual.
- Review the DNA Melting Thermodynamics Notes.
- If you need a review of Matlab fundamentals, see Matlab Fundamentals tutorial.
Matlab skills
- Element-by-element operations on arrays (+, -, .*, ./)
- Functions declared in an m-file
- Conditionals
- Functions that take a variable number of arguments
- Numerical differentiation
- Plotting data
Modeling dsDNA equilibrium concentration
We derived an expression for dsDNA concentration at a given temperature in class:
- $ K_{eq} = e^\left [\frac{\Delta S^{\circ}}{R} - \frac{\Delta H^{\circ}}{R T} \right ] $
- $ f = \frac{1 + C_T K_{eq} - \sqrt{1 + 2 C_T K_{eq}}}{C_T K_{eq}} $
Since this is a very complicated equation and we will use it many times, it makes sense to write a Matlab function.
dsDNA fraction function
The fraction of dsDNA is a function of 4 variables: ΔS°, ΔH°, temperature, and concentration. The DnaFraction function below takes four parameters to represent these quantities and an optional fifth parameter that causes the function to use a different value of the gas constant. Changing the fifth parameter allows the same function to operate with different unit systems.
A built-in MATLAB function in called nargin allows functions to accept a variable number of arguments. nargin returns the number of arguments that the function was called with. The DnaFraction function sets R to the default value of 1.987 if nargin returns a value of 4 or less. Otherwise, the function sets R to the value supplied by the caller.
The element-by-element divide operator in the body of the function makes it possible for DnaFraction to accept either a single temperature argument or a vector of temperature values. (As a general rule, use the ./ operator instead of / unless you intend to do a matrix divide.)
To use this function, save it in a file called "DnaFraction.m" (MATLAB requires that all functions be saved in a file that has the same name as the function appended with the extension ".m".) The file must reside in the current directory or another directory that is on your Matlab path. Function help should be placed in comments at the top of the file. Type help DnaFraction to see how this works.
% Returns the fraction of dsDNA in a solution containing equal concentrations
% of two complementary DNA oligos as a functino of total DNA concentration,
% temperature, entropy change, and enthalpy change.
% Gas constant is an optional parameter.
%
% USAGE: f = DnaFraction(Ct, T, DeltaS, DeltaH, <GasConstant>)
% RETURN VALUE: fraction of dsDNA
%
% Default units are molar, Kelvin, cal/mole, and cal/(mole-Kelvin). For
% other unit systems, supply the appropriate value of R in the optional
% fifth parameter. The default value is 1.987 cal/(degree K * mole).
function f = DnaFraction(Ct, T, DeltaS, DeltaH, GasConstant)
% Gas constant
if(nargin < 5) % determine if caller supplied R value or not
R = 1.987; % set to default: cal/(degree K * mole)
else
R = GasConstant; % otherwise use caller's value
end
% Compute Ct * Keq
CtKeq = Ct * exp(DeltaS / R - DeltaH ./ (R * T));
%now compute f
f = (1 + CtKeq - sqrt(1 + 2 * CtKeq)) ./ CtKeq;
% Written 4/9/2008 by SCW
Plot an ideal melting curve
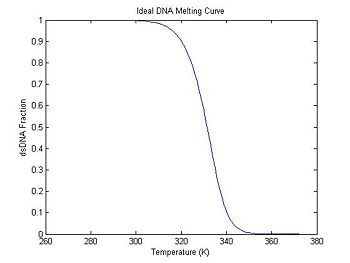
Does the DnaFraction function work as expected? A good way to test the function is to plot a melting curve generated by DnaFraction.
Matlab notes: Over the course of an interactive Matlab session, you may run several simulations with different parameters. Using a structure to keep the results of each simulation together is a good way to prevent the workspace from becoming disorganized. The struct function creates an empty structure. In the code below, a structure called ideal is created to hold the ideal melting curve data. (Since variables are dynamically allocated and typed in Matlab, the struct command is optional; however, explicitly creating the structure can make your code easier to read and better performing.)
Since DnaFraction accepts a vector temperature argument, an entire melting curve can be computed with a single call.
ideal = struct(); % create an empty structure to hold the results
ideal.temperature = (0:99) + 273.15; % temperature axis in Kelvin: 100 points(0-99C)
ideal.deltaS = -500; % cal/(mol K)
ideal.deltaH = -180E3; % cal/mol
ideal.concentration = 1E-6; % mol/L
% call DnaFraction function
% arguments: concentration, temperature vector, delta S, delta H
% (optional R argument not supplied)
ideal.dsDnaFraction = DnaFraction(ideal.concentration, ideal.temperature, ...
ideal.deltaS, ideal.deltaH);
plot(ideal.temperature, ideal.dsDnaFraction);
title('Ideal DNA Melting Curve');
xlabel('Temperature (K)');
ylabel('dsDNA Fraction');
Experiment with different values of ΔH° and ΔS° to see how the curve changes. You can use OligoCalc or another tool to estimate values for different DNA sequences.
One method of estimating Tm is to find the temperature where the dsDNA fraction equals 1/2. Another method is to differentiate the melting curve. Tm occurs at the peak of the derivative — where the dsDNA fraction is changing the fastest. (Why might you prefer one method to the other when estimating Tm from experimental data?)
Numerical differentiation
The fluorescence function fN is a sampled version of the continuous function f(T) such that fN = f(NΔT), where ΔT is the sampling interval (1° C, in this instance). One method for computing a numerical approximation to df/dT is the finite difference:
- $ {f'}_N = \frac{f_{N+1}-f_{N}}{\Delta T} $.
dF/dT is guaranteed to take on the value given by f'N at some point between NΔT and (N+1)ΔT; however, this happy coincidence can occur at any place in the interval. A simple but effective technique is to guess that equality occurs in the middle of the interval. This guess is close enough in most cases.
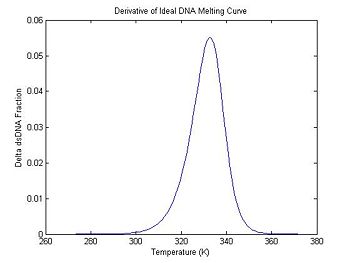
The code below computes the finite difference and stores it in the dDsDnaFraction field of ideal. It also generates an associated temperature vector (ideal.dTemperature) with values centered between the original temperature samples. Note that both vectors are one element shorter than the original data.
ideal.dTemperature = ideal.temperature(1:99) + 0.5; % create new temperature vector
ideal.dDsDnaFraction = diff(ideal.dsDnaFraction); % take the difference
plot(ideal.dTemperature, -1 * ideal.dDsDnaFraction);
title('Derivative of Ideal DNA Melting Curve');
xlabel('Temperature (K)');
ylabel('Delta dsDNA Fraction');
In the previous section, the plot shows that the dsDNA fraction equals 0.5 at about 332.5 degrees. The peak of the derivative also occurs at the same temperature. (The curve is plotted inverted.)
Set up simulation conditions and data structure
It will be convenient to set up a data structure with the simulation parameters and a time axis.
simulationLength = 900; % 15 minute simulation sampleRate = 1; % 1 Hz sample rate sim1 = struct(); % create empty struct for sim results sim1.concentration = 1E-6; % 1 micromolar concentration sim1.deltaS = -184; % cal / (mole-K) sim1.deltaH = -71E3; % cal / mole sim1.initialTemperature = 363; % 363 K = 90 C sim1.finalTemperature = 293; % approx. room temperature sim1.sampleRate = 1; % 1 Hz sample rate sim1.duration = 900; % seconds -- 15 minute experiment sim1.time = 0:(1./sampleRate):simulationLength; % create time vector (units: seconds)
Simulate sample temperature during an experimental run
The goal of the simulation is to produce two simulated voltage signals that resemble what you will measure in the lab. Since both of the voltages are functions of temperature, it makes sense to begin by modeling how the sample cools during an experimental run.
Sample cooling
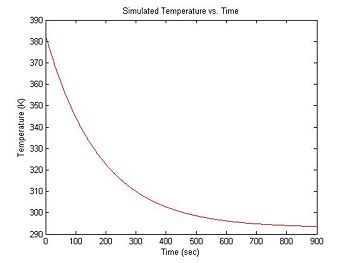
During each experimental run, the range of temperatures will be provided by natural cooling of the sample after it has been heated in a bath. At the beginning of an experimental run, the DNA + fluorescent dye sample is heated in a bath to around 90°C. Over a period of about 15 minutes, the sample cools to room temperature (about 20°C). The rate of cooling is proportional to the difference between the sample's temperature and the room temperature, so the sample cools more quickly at the start of the experiment than near the end. (It can be frustrating to wait for the final few degrees.)
Cooling can be approximated by an exponential function with a time constant of about 3 minutes. The equation for temperature (in °K) versus time is:
- $ T(t) = (T_i - T_f) e ^ {-\frac{t}{\tau}} + T_f $
where,
- T(t) is the temperature as a function of time,
- Ti is the initial temperature (after heating),
- Tf is the final (ambient) temperature,
- τ is the time constant.
In Matlab:
sim1.coolingConstant = 180;
% use exp function to model exponential cooling
sim1.temperature = ...
(sim1.initialTemperature - sim1.finalTemperature) .* ... % T_i - T_f *
exp(-sim1.time ./ sim1.coolingConstant) + ... % e^(-t/tau) +
sim1.finalTemperature; % T_f
plot(sim1.time, sim1.temperature, 'r');
xlabel('Time (sec)');
ylabel('Temperature (K)');
title('Simulated Temperature vs. Time');
If you have any questions about the element-by-element division operator in Matlab (./) see:this page.
RTD temperature sensor model
RTD and voltage divider circuit
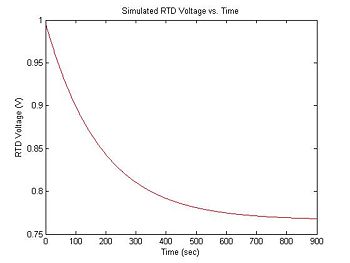
The resistance of the RTD is given by the equation RRTD = 1000 + 3.85(T - 273). In the experimental apparatus, the RTD is hooked up as one element of a voltage divider with another resistor, R. The power supply is 15 volts. Thus, the output voltage is: VRTD = 15 * RRTD/(R + RRTD). The following code calculates RTD voltage measurements from sim1.temperature and stores the result in sim1.V_RTD, assuming R = 20KΩ.
sim1.R_RTD = 1000 + 3.85 * (sim1.temperature - 273); % Compute RTD resistance in Ohms
sim1.V_RTD = 15 * sim1.R_RTD ./ (20E3 + sim1.R_RTD); % Compute V_RTD in Volts
plot(sim1.time, sim1.V_RTD, 'r');
xlabel('Time (sec)');
ylabel('RTD Voltage (V)');
title('Simulated RTD Voltage vs. Time');