20.309: Biological Instrumentation and Measurement

DNA in solution
| $ \bullet $ |
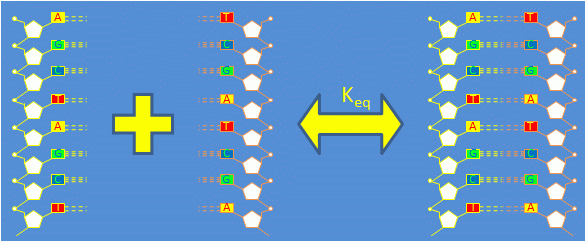
Consider a solution containing equal quantities of complementary single stranded DNA (ssDNA) oligonucleotides $ \left . A \right . $ and $ \left . A' \right . $.
|
| $ \bullet $ |
Complementary ssDNA strands bond to form double stranded DNA (dsDNA). The reaction is governed by the equation $ 1 A + 1 A' \Leftrightarrow 1 A \cdot A' $
|
| $ \bullet $ |
The forward reaction in which two ssDNA oligos combine to form dsDNA is called annealing. The reverse process is called thermal denaturation or melting.
|
| $ \bullet $ |
At low temperatures, dsDNA is favored. As the temperature rises, dsDNA increasingly separates into its component ssDNA oligos. (Think about why with respect to enthalpic and entropic considerations.)
|
| $ \bullet $ |
The melting temperature, $ \left . T_m \right . $, is defined to be the point where half of the dsDNA is denatured.
|
| $ \bullet $ |
Short sequences of about 10-40 base pairs (such as those used in the DNA Melting lab) tend to denature all at once. Longer sequences may melt in segments.
|
| $ \bullet $ |
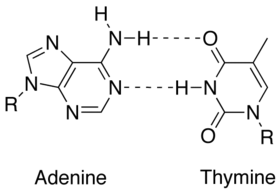
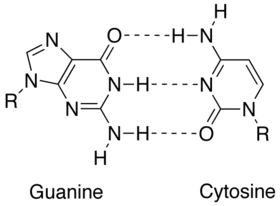
Less energy is required to split the double hydrogen bond of A-T pairs than the triple bond of G-C pairs. Thus, A-T rich sequences tend to melt at lower temperatures than G-C rich ones.[1]
|
Several web tools are available to predict the melting temprature. (See, for example, DINA Melt or Oligocalc.)
Fundamental equilibrium relationships
| $ \bullet $ |
The concentrations of the reaction products are related by the equilibrium constant: $ K_{eq} = \frac{\left [ A \cdot A' \right ]}{\left [ A \right ] \left [ A' \right ]} $
|
| $ \bullet $ |
The value of $ \left . K_{eq} \right . $ is a function of temperature. We can equate the fundamental definition of the standard free energy change with its relationship to the equilibrium constant in solution:
|
- $ \begin{align} \Delta G^{\circ} & = \Delta H^{\circ} - T \Delta S^{\circ}\\ & = -R T \ln K_{eq}\\ \end{align} $
- where
- $ \Delta G^{\circ} $ is the standard change in free energy
- $ \Delta H^{\circ} $ is the standard enthalpy change
- $ \left . T \right . $ is the temperature
- $ \Delta S^{\circ} $ is the standard entropy change
- $ \left . R \right . $ is the gas constant
| $ \bullet $ |
Solving for $ \left . K \right . $:
|
- $ K_{eq} = e^\left [\frac{\Delta S^{\circ}}{R} - \frac{\Delta H^{\circ}}{R T} \right ] \quad (1) $
Note that the above equation can be differentiated with respect to temperature to yield the (perhaps once!) familiar van't Hoff equation.
Theoretical relation of dsDNA fraction and thermodynamic parameters
| $ \bullet $ |
In the lab, the fraction of dsDNA will be measured with a fluorescent dye that preferentially binds to dsDNA. As such, it will be useful to derive an equation that relates the fraction of dsDNA to temperature and the thermodynamic parameters.
|
| $ \bullet $ |
Let $ \left . C_{SS} \right . $ represent the concentration of either single stranded oligonucleotide: $ C_{SS} = {\left [ A \right ] = \left [ A' \right ]} $.
|
| $ \bullet $ |
Similarly, let $ \left . C_{DS} \right . $ be the concentration of double stranded DNA: $ C_{DS} = {\left [ A \cdot A' \right ]} $
|
| $ \bullet $ |
$ \left . C_T \right . $ is the total concentration of DNA strands. $ \left . C_T = 2 C_{SS} + 2 C_{DS}\right . $
|
| $ \bullet $ |
Let $ \left . f \right . $ be the fraction of total DNA that is double stranded
|
- $ f = \frac{2 C_{DS}}{C_T} = \frac{C_T - 2 C_{SS}}{C_T} = 1 - 2 \frac{C_{SS}}{C_T} $
| $ \bullet $ |
Therefore, $ C_{SS} = \frac{(1 - f)C_T}{2} $
|
| $ \bullet $ |
Now we can solve for $ \left . K \right . $ in terms of $ \left . f \right . $ and $ \left . C_T \right . $:
|
- $ K_{eq} = \frac{C_{DS}}{C_{SS}^2} = \frac{f C_T / 2}{ [(1 - f) C_T / 2] ^ 2} = \frac{2 f}{(1 - f)^2 C_T} $
| $ \bullet $ |
At the melting point, $ f = \frac{1}{2} $ by definition and thus $ K_{eq} = \frac {4}{C_T} $.
|
| $ \bullet $ |
Substituting for Keq from equation 1:
|
- $ e^\left [\frac{\Delta S}{R} - \frac{\Delta H}{R T} \right ] = \frac{2 f}{(1 - f)^2 C_T} \quad (2) $
| $ \bullet $ |
Taking the log of both sides and solving for $ \left . T \right . $:
|
- $ T(f) = \frac{\Delta H^{\circ}}{\Delta S^{\circ}-R \ln(2f/C_T(1-f)^2)} $
We now know temperature as a function of dsDNA fraction for a given total DNA strand concentration and DNA identity (therefore ΔH, etc.).
Simulating DNA melting for tractable calculation of dsDNA fraction
| $ \bullet $ |
For simulating DNA melting experiments, it will be convenient to have an expression for $ \left . f \right . $ in terms of $ \left . T \right . $. Unfortunately, this gets pretty yucky. On the bright side, Matlab and Python are good at calculating yuck.
|
| $ \bullet $ |
Taking the log of both sides of equation 2 (after re-substiting in equation 1 for simplicity) and using the quadratic formula (eliminating the nonphysical root):
|
- $ f = \frac{1 + C_T K_{eq} - \sqrt{1 + 2 C_T K_{eq}}}{C_T K_{eq}} $
| $ \bullet $ |
Substituting from equation 1 gives the desired result.
|
- $ f = \frac{1 + C_T e^\left [\frac{\Delta S^{\circ}}{R} - \frac{\Delta H^{\circ}}{R T} \right ] - \sqrt{1 + 2 C_T e^\left [\frac{\Delta S^{\circ}}{R} - \frac{\Delta H^{\circ}}{R T} \right ]}}{C_T e^\left [\frac{\Delta S^{\circ}}{R} - \frac{\Delta H^{\circ}}{R T} \right ]} $
See the pages DNA Melting Part 1: Simulating DNA Melting - Basics. And if you're interested in a Python implementation see Python:Simulating DNA Melting
References
- ↑ Breslauer et al., Predicting DNA duplex stability from the base sequence PNAS 83: 3746, 1986



