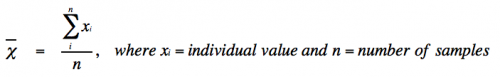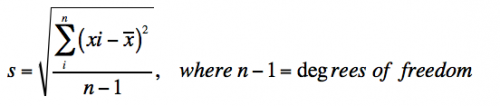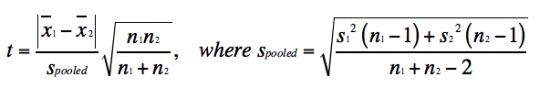20.109(S19):Complete data analysis (Day7)

Introduction

Today is the final laboratory session for Module 1! You have completed all of the bench work for your research; however, there is still data analysis to complete for your experiments. In addition to plotting and normalizing the data, you will complete statistical analysis to determine the significance of your results.

Statistics are mathematical tools used to analyze, interpret, and organize data. The specific tools that you will use are confidence intervals (CI) and the Student's t-test. To begin, review the following definitions:

• Mean (or average) is defined as:

• With infinite data, the mean (χ_ι) approaches the true mean (μ).
• Standard deviation measures the variation in the data and is defined as:

• With infinite data, the standard deviation (s) approaches the true standard deviation (σ).

Because standard deviation is only justified when sufficient data have been collected to generate a normal curve, you will use confidence intervals to report the likelihood that your results predict the true mean. A confidence interval is a defined interval that is calculated to define the true mean to a specified level of confidence. Simply, it is possible to define a range in your data set that likely contains the true mean based on the calculated mean.

• Confidence interval is defined as:

In your data, you should use the CI to generate error bars due the low n. Be sure to report which confidence level was used to calculate the intervals reported. So, what does this all mean in regard to the data you will report? As an example, if the calculated χ_ι of a data set equals 80 au there is a 95% chance the μ is between 50 au and 110 au, where au = arbitrary units. And how does this relate to s? If you know the μ, the σ represents a 68% confidence interval.

Lastly, you will use Student's t test to report if your data are statistically different between treatments.

• Student's t test is defined as:

The value you calculate with the Student's t test equation is referred to as t_calculated. This t_calculated value is compared to the t_tabulated value in the the t table, according to the appropriate n - 1 using the p-value for the two-tailed distribution (which assumes that you do not know how the data will shift). If the t_calculated value is greater than the t_tabulated, then the data sets are significantly different at the specific p-value. So, what does this all mean in regard to the data you will report? As an example, if the t_calculated for a data set with n - 1 = 10 is 3 (given that the t_tabulated is 2.228), then the data sets are different with a p-value ≤ 0.05. Which means that there is less that a 5% chance that the data sets are the same.

Part 1: Practice statistical analysis

Review these data from an experiment where cells were exposed to increasing amounts of radiation. Your goal is to determine if a statistically significant amount of DNA damage was induced. For the purpose of this exercise, the values in the spreadsheet are in arbitrary units of 'DNA damage', where the higher numbers indicate more damage.

When interpreting the statistics, consider how you may use the information to convince someone that the DNA damage was significant. You may find this spreadsheet, originally created by Prof. Bevin Engelward and modified by the 20.109 staff, helpful for this exercise. At a minimum, you should post a bar plot of the data with 95% confidence intervals and indicate if there is a statistically significant difference (i.e. provide a p-value) between conditions in your Benchling notebook.

Part 2: Complete data analysis

Use the tools above to analyze the data for your PPIase and DSF experiments. The figures / analyses in your Data summary should include measures of variability (i.e. confidence intervals) and significance (i.e. p-values).

Navigation links

Next day: Practice tissue culture techniques and prepare cells for RNA purification

Previous day: Confirm ligand binding using differential scanning fluorimetry assay