Difference between revisions of "Optical Microscopy Part 3: Resolution and Stability"
MAXINE JONAS (Talk | contribs) |
MAXINE JONAS (Talk | contribs) (→Instructions) |
||
| Line 78: | Line 78: | ||
==Instructions== | ==Instructions== | ||
| + | |||
| + | ===Measuring resolution=== | ||
| + | One of the most commonly used definitions of resolution is the distance between two point sources in the sample plane such that the peak of one source’s image falls on the first minimum of the other source’s image. This suggests a procedure for measuring resolution: image a point source; measure the peak-to-trough distance; and divide by the magnification. In this part of the lab, you will use this method to estimate the resolution of your microscope. | ||
| + | |||
| + | A practical problem with this method is that true point sources are difficult to come by. If you are using a telescope, stars are readily available approximate point sources. In microscopy, people usually use tiny, fluorescent beads with diameters of 100-190 nm. These beads are small enough to be considered point sources. You will use nonlinear regression to estimate the resolution of your microscope from an image of the tiny beads. Unfortunately, beads small enough for this purpose are not very bright. Imaging them can be challenging. Your microscope must be aligned very well to get good results. | ||
| + | |||
| + | You will use image processing functions to locate the beads in your image and fit a Gaussian function to them. Gaussians are more amenable to nonlinear regression than Bessel functions, and they are a very good approximation. It is straightforward to convert the Gaussian parameters to Rayleigh resolution. (See [[Converting Gaussian fit to Rayleigh resolution]].) | ||
| + | |||
| + | # Make an image of a sample of 100 or 190 nm fluorescent beads with the 40X objective. | ||
| + | #* Use 12-bit mode on the camera and make sure to save the image in a format that preserves all 12 bits. | ||
| + | #* Use <code>imhist</code> to ensure that the image is exposed properly. | ||
| + | #** Since there are a very small number of bright pixels, plot the histogram counts on a logarithmic scale. | ||
| + | #* '''Include the image in your lab report.''' | ||
| + | # Use image processing functions to locate non-overlapping, single beads in the image. | ||
| + | # Use nonlinear regression to fit a Gaussian to each bead image. | ||
| + | # Convert the Gaussian parameters to resolution. | ||
| + | # '''Report the results in your lab report.''' | ||
| + | #* [[MATLAB: Estimating resolution from a PSF slide image|This page]] has example MATLAB code. | ||
| + | #* '''Discuss how the measured resolution compares with the theoretical value.''' | ||
===Stability of microscope for particle tracking=== | ===Stability of microscope for particle tracking=== | ||
Revision as of 17:09, 14 February 2014
Contextual Background
- Read background references
- R. Newburgh, Einstein, Perrin, and the reality of atoms: 1905 revisited, Am. J. Phys. (2006). A modern replication of Perrin's experiment. Has a good, concise appendix with both the Einstein and Langevin derivations.
- A. Einstein, On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat, Annalen der Physik (1905).
- M. Haw, Colloidal suspensions, Brownian motion, molecular reality: a short history, J. Phys. Condens. Matter (2002).
- E. Frey and K. Kroy, Brownian motion: a paradigm of soft matter and biological physics, Ann. Phys. (2005).
- Random Force & Brownian Motion — 60 Symbols
Shot noise and centroid finding
 Shot noise is a fluctuation that affects all light intensity measurements, including microscopic images recorded with a CCD camera. [1] It is a consequence the discrete and the stochastic nature of photon emission. Poisson statistics provide an excellent model for shot noise. The standard deviation of a Poisson-distributed random variable is equal to the square root of its average value. Thus, the lowest possible signal to noise ratio of an intensity measurement is equal to the square root of the average number of photons (intensity). The simulated images above show the effect of shot noise on the image of a fluorescent microsphere with a radius of 10 pixels for several values of intensity.
Shot noise is a fluctuation that affects all light intensity measurements, including microscopic images recorded with a CCD camera. [1] It is a consequence the discrete and the stochastic nature of photon emission. Poisson statistics provide an excellent model for shot noise. The standard deviation of a Poisson-distributed random variable is equal to the square root of its average value. Thus, the lowest possible signal to noise ratio of an intensity measurement is equal to the square root of the average number of photons (intensity). The simulated images above show the effect of shot noise on the image of a fluorescent microsphere with a radius of 10 pixels for several values of intensity.
One method to estimate the position of a microsphere in an image is to compute an intensity-weighted centroid (also called the center of mass). Intensity-weighted centroids can provide locations accurate to a fraction of a pixel. Shot noise causes random variation in the pixel intensities, which perturbs the centroid. Repeated localizations of a stationary particle will exhibit random variation. Deriving an analytical expression for the variation is tedious. Happily, patient people with exceptional mathematical abilities have taken the time to do so. (See, for example, this reference: Jia, Jiankun Yang, and Xiujian Li. Minimum variance unbiased subpixel centroid estimation of point image limited by photon shot noise.). The variation in the centroid is approximately proportional to the square root of intensity.
As a result, the diffusion coefficient measured by taking intensity weighted centroids of a perfectly stationary particle will not be zero. The measured diffusion coefficient of a non stationary particle will be systematically increased.
Here is the code that generated the simulated images:
figure
maximumIntensity = [1e6 1e4 1e2 1e1 1e0];
radius = 10;
imageSize = [40 40];
for ii = 1:length(maximumIntensity)
subplot(1, length(maximumIntensity), ii)
imshow(poissrnd(SimulateFluorescentParticleImage(imageSize ./ 2, maximumIntensity(ii), ...
radius, imageSize)) ./ maximumIntensity(ii));
title(['SNR = ' num2str(sqrt(maximumIntensity(ii)))]);
end
function [ OutputImage ] = SimulateFluorescentParticleImage( CentroidList, Intensity, ...
Raduis, ImageSize )
numberOfParticles = size(CentroidList,1);
OutputImage = zeros(ImageSize);
if(length(Raduis) == 1)
Radius = Raduis * ones(1, numberOfParticles);
end
if(length(Intensity) == 1)
Intensity = Intensity * ones(1, numberOfParticles);
end
for ii=1:numberOfParticles
OutputImage = OutputImage + DrawParticle(CentroidList(ii, 1), CentroidList(ii, 2), ...
Radius(ii), Intensity(ii), ImageSize(1), ImageSize(2));
end
end
Brownian motion
This section was adapted from http://labs.physics.berkeley.edu/mediawiki/index.php/Brownian_Motion_in_Cells.
If you have ever looked at an aqueous sample through a microscope, you have probably noticed that every small particle you see wiggles about continuously. Robert Brown, a British botanist, was not the first person to observe these motions, but perhaps the first person to recognize the significance of this observation. Experiments quickly established the basic features of these movements. Among other things, the magnitude of the fluctuations depended on the size of the particle, and there was no difference between "live" objects, such as plant pollen, and things such as rock dust. Apparently, finely crushed pieces of an Egyptian mummy also displayed these fluctuations.
Brown noted: [The movements] arose neither from currents in the fluid, nor from its gradual evaporation, but belonged to the particle itself.
This effect may have remained a curiosity had it not been for A. Einstein and M. Smoluchowski. They realized that these particle movements made perfect sense in the context of the then developing kinetic theory of fluids. If matter is composed of atoms that collide frequently with other atoms, they reasoned, then even relatively large objects such as pollen grains would exhibit random movements. This last sentence contains the ingredients for several Nobel prizes!
Indeed, Einstein's interpretation of Brownian motion as the outcome of continuous bombardment by atoms immediately suggested a direct test of the atomic theory of matter. Perrin received the 1926 Nobel Prize for validating Einstein's predictions, thus confirming the atomic theory of matter.
Since then, the field has exploded, and a thorough understanding of Brownian motion is essential for everything from polymer physics to biophysics, aerodynamics, and statistical mechanics. One of the aims of this lab is to directly reproduce the experiments of J. Perrin that lead to his Nobel Prize. A translation of the key work is included in the reprints folder. Have a look – he used latex spheres, and we will use polystyrene spheres, but otherwise the experiments will be identical. In addition to reproducing Perrin's results, you will probe further by looking at the effect of varying solvent molecule size.
Diffusion coefficient of microspheres in suspension
According to theory,[2][3][4][5] the mean squared displacement of a suspended particle is proportional to the time interval as: $ \left \langle {\left | \vec r(t+\tau)-\vec r(t) \right \vert}^2 \right \rangle=2Dd\tau $, where r(t) = position, d = number of dimensions, D = diffusion coefficient, and $ \tau $= time interval.
Instructions
Measuring resolution
One of the most commonly used definitions of resolution is the distance between two point sources in the sample plane such that the peak of one source’s image falls on the first minimum of the other source’s image. This suggests a procedure for measuring resolution: image a point source; measure the peak-to-trough distance; and divide by the magnification. In this part of the lab, you will use this method to estimate the resolution of your microscope.
A practical problem with this method is that true point sources are difficult to come by. If you are using a telescope, stars are readily available approximate point sources. In microscopy, people usually use tiny, fluorescent beads with diameters of 100-190 nm. These beads are small enough to be considered point sources. You will use nonlinear regression to estimate the resolution of your microscope from an image of the tiny beads. Unfortunately, beads small enough for this purpose are not very bright. Imaging them can be challenging. Your microscope must be aligned very well to get good results.
You will use image processing functions to locate the beads in your image and fit a Gaussian function to them. Gaussians are more amenable to nonlinear regression than Bessel functions, and they are a very good approximation. It is straightforward to convert the Gaussian parameters to Rayleigh resolution. (See Converting Gaussian fit to Rayleigh resolution.)
- Make an image of a sample of 100 or 190 nm fluorescent beads with the 40X objective.
- Use 12-bit mode on the camera and make sure to save the image in a format that preserves all 12 bits.
- Use
imhistto ensure that the image is exposed properly.- Since there are a very small number of bright pixels, plot the histogram counts on a logarithmic scale.
- Include the image in your lab report.
- Use image processing functions to locate non-overlapping, single beads in the image.
- Use nonlinear regression to fit a Gaussian to each bead image.
- Convert the Gaussian parameters to resolution.
- Report the results in your lab report.
- This page has example MATLAB code.
- Discuss how the measured resolution compares with the theoretical value.
Stability of microscope for particle tracking
The accuracy of optical particle tracking may be limited by mechanical and optical phenomena. Vibration and drift are a source of additive noise. Shot noise and CCD readout noise in the image of a particle bring about uncertainty in the estimate of its centroid. Excessive vibration can frequently be corrected by improving the mechanical support structure of the instrument. Most stages can be locked to reduce drift. Shot noise is fundamental; however, its relative contribution to the total signal can be minimized by ensuring that the optical system is functioning at peak efficiency.
Before attempting to make measurements with particle tracking, it is essential to determine the performance characteristics of the instrument to be used. This can be accomplished by measuring a specimen with known characteristics. Perhaps the most foolproof choice is a sample with fixed particles. Any measured variation in the fixed sample is noise, if your analysis is done properly.
- To verify that your system is sufficiently stable for accurate particle tracking, monitor a dry specimen containing 1μm fluorescent beads.
- Bring a slide with fixed beads into focus. Choose a field of view in which you can see at least 3 beads with the 40× objective. Limit the field of view to only those beads by choosing a region of interest (ROI).
- Track the beads for 3 minutes and save the centroids with a frame rate of your choice and make a note of it.
- Use the Matlab function
track(check out the Stellar Reading Materials sections for an example, and be sure to limit the algorithm to a small region of interest around the beads, otherwise Matlab will struggle!) to separate the centroids into individual trajectories, $ \vec r_n(t) $, where $ t = nT $ and $ T $ is the inverse of the frame rate you set above. - Compute the difference of the trajectories for two particles, $ \vec r_-(t) = \vec r_1(t) - \vec r_2(t) \sqrt{2} $. (Why is the square root of 2 necessary?)
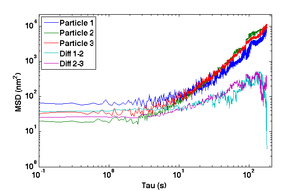
- Compute and plot the mean squared displacement (MSD) of $ r_- $ as a function of time interval and compare to the MSD of the actual particle tracks, $ \left \langle {\left | \vec r(t+\tau)-\vec r(t) \right \vert}^2 \right \rangle $ for intervals $ \tau=nT $ up to 180 s.
- Why does the MSD of the particle trajectory increase while the difference trajectory stays about the same?
- Can you take advantage of this property to decrease the error in measurements of unknown samples?
- Make any necessary adjustments to your microscope and repeat this particle-tracking procedure to attain sufficient stability:
- The MSD from the difference trajectory should start out less than 100 nm2 at t = 1 s and still be less than 1000 nm2 for t = 180 s.
Estimating the diffusion coefficient by tracking suspended microspheres
1. Track some ~1μm Nile Red Spherotech polystyrene beads in water-glycerin mixtures (Samples A, B and C contain 0%, 30% and 50% glycerin, respectively).
- Notes: Fluorescent microspheres have been mixed for you by the instructors into water-glycerin solutions A, B, C, and D. (a) Vortex the stock Falcon tube, and then (b) transfer the bead suspension into its imaging chamber (consisting of a microscope slide, double-side tape delimiting a 2-mm channel, and a 22x40mm No. 1.5 coverslip).
- Tip: Do not choose to monitor particles that remain stably in focus: these are likely to be 'sitting on the coverslip' and their motion will not be representative of diffusion in the viscous water-glycerol fluid.
2. Estimate the diffusion coefficient of these samples: $ \left \langle {\left | \vec r(t+\tau)-\vec r(t) \right \vert}^2 \right \rangle=2Dd\tau $, where r(t) = position, d = number of dimensions, D = diffusion coefficient, and $ \tau $= time interval. Use Sample A to verify that your algorithm correctly calculates the viscosity of water at the lab temperature (check the temperature on the clock on the wall or by other means).
Example images:
Report
Remember to include uncertainty and a discussion of error sources for all numerical results.
Microscope stability
- Provide X-Y plots of sum and difference tracks for fixed particles.
- Provide plots of MSD versus time interval for sum and difference tracks1.
- Provide a bullet point outline of your data analysis methodology.
- Comment on observed vs. expected data trend.
Diffusion coefficient and viscosity
- Estimate diffusion coefficient, viscosity for each water-glycerin mixture sample.
- Comment on results, specifically how they are influenced by microscope stability and resolution.
- Comment extensively on sources of error and approaches to minimize them, both utilized and proposed.
- Provide a bullet point outline of all calculations and data processing steps.
Optical microscopy lab
Code examples and simulations
- Converting Gaussian fit to Rayleigh resolution
- MATLAB: Estimating resolution from a PSF slide image
- Matlab: Scalebars
- Calculating MSD and Diffusion Coefficients
Background reading
- Geometrical optics and ray tracing
- Physical optics and resolution
- Optical aberrations
- Aperture and field stops
- Optical detectors, noise, and the limit of detection
- Manta G032 camera measurements
- Understanding log plots
References
- ↑ There are a few exotic methods, such as amplitude-squeezed light that reduce noise below the shot noise level.
- ↑ A. Einstein, On the Motion of Small Particles Suspended in Liquids at Rest Required by the Molecular-Kinetic Theory of Heat, Annalen der Physik (1905).
- ↑ E. Frey and K. Kroy, Brownian motion: a paradigm of soft matter and biological physics, Ann. Phys. (2005). Published on the 100th anniversary of Einstein’s paper, this reference chronicles the history of Brownian motion from 1905 to the present.
- ↑ R. Newburgh, Einstein, Perrin, and the reality of atoms: 1905 revisited, Am. J. Phys. (2006). A modern replication of Perrin's experiment. Has a good, concise appendix with both the Einstein and Langevin derivations.
- ↑ M. Haw, Colloidal suspensions, Brownian motion, molecular reality: a short history, J. Phys. Condens. Matter (2002).