Physical optics and resolution
Overview
In the seventeenth century, Antonie van Leeuwenhoek and Robert Hooke made dramatic improvements in microscopes. Their work brought about many fundamental discoveries. Both men documented the existence of cells, one of the most significant observations in the history of science. But Hooke and van Leeuwenhoek didn't get much further than that. Why didn't they discover organelles, proteins, or atoms?
Two things are required to visualize something with a microscope: resolution and contrast. Resolution is a measure of the finest detail that can be seen through an optical system. Alone, resolution is insufficient to make something visible. There must also be contrast — some kind of difference between the thing you want to see and whatever else makes up the rest of the sample.
Hooke and van Leeuwenhoek couldn't see things much smaller than cells because their microscopes had very bad optical aberrations. Aberrations are technical shortcomings that distort images made by optical systems. Over the intervening three and a half centuries, engineers developed clever designs that reduce optical aberrations to arbitrarily small levels (in some cases, at arbitrarily large price points).
Even assuming that all the aberrations had been eliminated from their microscopes, though, the early microscopists still would not have glimpsed a protein molecule or an atom. In the ray tracing model, rays passing through a lens come together at a point in the image plane. In actuality, light passing through an aperture undergoes a modification called diffraction that spreads the point predicted by the ray model into a disk of light. This spreading causes points of light to intrude on their neighbors, blurring the image.
This page explains how diffraction affects light, the quantitative definition of resolution, how to calculate the theoretical resolution of a microscope, and some methods for generating contrast.
Diffraction and resolution
To ray optics, or geometrical optics, that provide intuition and equations to account for reflection and refraction and for imaging with mirrors and lenses, we can add the concepts of wave optics, also dubbed physical optics, and thereby grasp phenomena including interferences, diffraction, and polarization.
Maxwell's equations
- The set of partial differential equations unified under the term 'Maxwell's equations' describes how electric $ \vec E $ and magnetic $ \vec {B} $ fields are generated and altered by each other and by charges and currents.
- $ \nabla \cdot \vec E = {\rho \over \varepsilon_0} $
- $ \nabla \cdot \vec B = 0 $
- $ \nabla \times \vec E = - {\partial \vec B \over \partial t} $
- $ \nabla \times \vec B = \mu_0 \left ( \vec J + \varepsilon_0 {\partial \vec E \over \partial t} \right ) $
- where ρ and $ \vec J $ are the charge density and current density of a region of space, and the universal constants $ \varepsilon_0 $ and $ \mu_0 $ are the permittivity and permeability of free space. The nabla symbol $ \nabla $ denotes the three-dimensional gradient operator, $ \nabla \cdot $ the divergence operator, and $ \nabla \times $ the curl operator.
- In vacuum where there are no charges (ρ = 0) and no currents ($ \vec J = \vec 0 $), Maxwell's equations reduce to
- $ \nabla^2 \vec E = {1 \over c^2}{\partial^2 \vec E \over \partial t^2} $
- $ \nabla^2 \vec B = {1 \over c^2}{\partial^2 \vec B \over \partial t^2} $
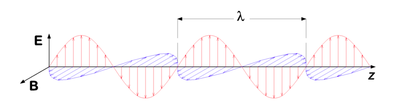
- At large distances from the source, a spherical wave may be approximated by a plane wave, of direction of propagation $ \vec E\ \times\ \vec B $. In space and time, the electric and magnetic fields vary sinusoidally:
- $ \vec E (\vec r, t) = \vec E_0 \cos ({\vec k \cdot \vec r} - \omega t + \phi_0) $
- $ \vec B (\vec r, t) = \vec B_0 \cos ({\vec k \cdot \vec r} - \omega t + \phi_0) $
- where $ t $ is time (in seconds), $ \omega $ is the angular frequency (in radians per second), $ \vec k = (k_x,\ k_y,\ k_z) $ is the wave vector (in radians per meter), and $ \phi_0 $ is the phase angle (in radians). The wave vector is related to the angular frequency by $ k = \left\vert \vec k \right\vert = { \omega \over c } = { 2 \pi \over \lambda } $, where k is the wavenumber and λ is the wavelength.
Interferences
Key results from the theory of interactions of wave lights are:
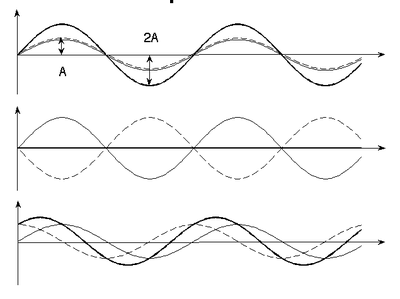
Principle of linear superposition
The (vector) electric and magnetic fields from each source of an electromagnetic wave add.
|
|
| |
|
Huygens-Fresnel principle
As a wavefront propagates, each point on the wavefront acts as a point source of secondary spherical light waves.
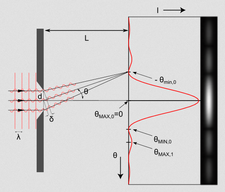
Fraunhofer and Fresnel diffractions
The Huygens-Fresnel principle can be used to solve diffraction of a plane wave as it passes through a slit by putting many sources along the wavefront. Fraunhofer diffraction refers to the pattern when observed far from the slit (far-field diffraction) or through a lens, while Fresnel diffraction refers to the near-field counterpart.
| Diffraction pattern through a single slit | |
|

|
Resolution
Airy discs
- Diffraction through a circular pinhole creates Airy discs, whose intensity on the imaging screen follows the equation
- $ I ( \theta ) = I_0 \left ( {2 J_1 {(ka \sin \theta)} \over ka \sin \theta}\right ) ^2 $
- where J1 is the Bessel function of first kind, k = 2 π / λ, and θ is the angle from the direction of light propagation.
- The half-angle beam spread to first minimum, θ, occurs at
- $ \sin \theta = 1.22 {\lambda \over D} $
- with λ the wavelength of the light and D the diameter of the round aperture (pinhole).
Rayleigh resolution
- Rayleigh criterion (a somewhat arbitrary definition of resolution!) claims that two points are resolved if the maximum of one Airy disk lies at the first zero of the other.
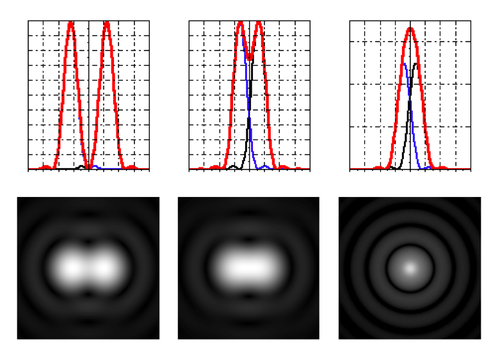
- For small angles,
- $ R \approx 1.22 {\lambda f \over D} \approx 0.61 {\lambda \over NA} $
- where $ R $ is the separation of the images of the two point objects on the film, $ f $ is the distance from the lens to the film, and NA = n sin α is the numerical aperture of the imaging lens.
- It ensues that it is very difficult to achieve a resolution R less than ~ 160 nm with a light microscope (even with a big lens of small focal length f and sin α ~ 1, even with oil immersion granting n ~ 1.5, and blue visible light of λ ~ 400 nm)!
- Be aware that since real-life lenses are of finite dimensions, diffraction through a circular aperture is unavoidable and does take place in your microscope. Diffraction through a circular aperture can be simulated by convolution of the original image with a simulated Airy disk.
Enhancing image contrast
Optical microscopy, involving visible light either transmitted through or reflected by the sample, is fettered by three categories of limitations:
- Diffraction limits resolution to ~ 0.2 μm (see above).
- Only strongly absorbing (dark) or strongly refracting objects can be successfully imaged.
- Background signal from points outside of the focal plane undermine image contrast.
To overcome these limitations, several specific microscopy techniques have been developed. Good overviews can be found at zeiss.com [1] and fsu.edu [2] (where the figures in this section were taken from) if you're interested in learning more.
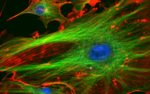
Fluorescence microscopy
Fluorescence microscopy has greatly contributed to our understanding of biological systems over the past few decades, as forays were made in parallel in molecular probe development and imaging techniques. Fluorescence has enabled researchers
- to identify and distinguish molecules of interest (such as filamentous actin in the 20.309 lab),
- to monitor intracellular processes (such as calcium ion signaling, transmembrane migration, protein interactions, nitrogen oxidation),
- to achieve sub-diffraction resolution.
Light
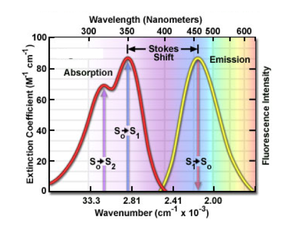
The principle of fluorescence imaging consists in illuminating fluorophores with a specific wavelength (or narrow range of wavelengths) which they absorb, causing them in turn to emit light of longer wavelengths. Fluorophore electrons indeed get excited by the photonic energy of incident light from their ground state to higher singlet excited states, before relaxing down to the ground state, thereby releasing photonic energy in the form of red-shifted light.
|
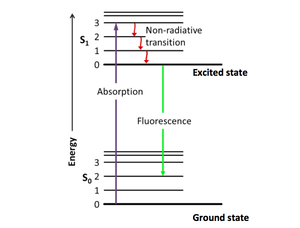
|
| Example of excitation and emission spectra for the fluorophore quinine | Jablonski diagram describing relaxation mechanisms, including fluorescence, for excited state molecules |
In 20.309, the fluorophores we use will emit light in the orange-red region of the visible spectrum (550-610 nm) when excited by green LED (540-560 nm).
In any fluorescence system, a key concern is viewing only the emitted fluorescence photons, and eliminating any background light, especially from the illumination source. Two optical elements address the problem.
- A dichroic mirror reflects light of one wavelength (green, in our case), and passes light of another (red).
- A barrier filter blocks a particular spectral region extremely well (e.g. all wavelengths shorter than its cut-off in the orange region of the visible light spectrum)
Sample
For fluorescence imaging, specimen preparation entails either production of fluorescently labeled proteins by recombinant gene expression, or exogenous addition of fluorescent tags.
Limitations
Keep in mind the following points as you opt for a fluorescence imaging approach:
- How does the probe work? What properties or events does it measure?
- How does the probe label the cell or its molecules? Is its incorporation fatal to the cell (because of toxicity, or from the need to use detergent to break the cell membrane barrier and introduce the fluorophores into the cell)?
- How biologically relevant and accurate are the deductions enabled by the fluorescent probe? Do the bulky fluorophores hinder, skew, or modify the inherent, native molecular interactions of otherwise unlabeled structures?
- Is the probe destined to sequestration or exocytosis by the cell because of its coating?
- How bright will the signal from a single probe be? will single-molecule detection be possible, or will the signal be an aggregate of many fluorophores' contributions?
- How fast will photobleaching of the probe occur? What laser excitation power is appropriate for your purposes?
- Will autofluorescence (more marked in the blue spectrum) decrease the contrast of your images?
- ... and of course: How will signal detection and imaging be accomplished? Are the speed, resolution and sensitivity of the detecting apparatus adequate?
Techniques
High-resolution microscopy techniques are further discussed on this wiki page and include key advances in the arenas of
- Epifluorescence
- FRET
- FRAP
- Total internal reflection
- Standing wave illumination
- STORM
- Two-photon & confocal imaging for 3D depth resolution on sample information.
Optical microscopy lab
Code examples and simulations
- Converting Gaussian fit to Rayleigh resolution
- MATLAB: Estimating resolution from a PSF slide image
- Matlab: Scalebars
- Calculating MSD and Diffusion Coefficients
Background reading
- Geometrical optics and ray tracing
- Physical optics and resolution
- Optical aberrations
- Aperture and field stops
- Optical detectors, noise, and the limit of detection
- Manta G032 camera measurements
- Understanding log plots