Input and output impedance
Overview
What happens when we connect one circuit component to another? Sometimes the circuit component doesn't behave in the same way when it is by itself versus when it is connected to another component. To understand how the circuit will behave, we must consider the input and output impedances of the different parts. The output impedance refers to the impedance, or opposition to current flow, of the component that often bears an electrical source to "drive" a load component. Meanwhile, the input impedance refers to the load component's opposition to current flowing in from the electrical source. In many cases, you will want to have a high input impedance relative to output impedance, and you will see why in the following sections.
Battery example
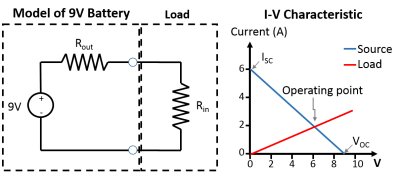
Let's look at an example of connecting a battery to a resistor. When we see a 9V battery, we often think it should output 9V from its terminals. It truly does, but only when it's not sourcing any current. It turns out that there is some internal impedance inside the battery that prevents the output voltage from remaining at 9V once current starts to flow. We can thus model the battery as a pure voltage source in series with a resistor, where the resistance value $ R_{out} $ is equal to the output impedance of the battery. Here is an example of a 9V battery's I-V curve (current-voltage relationship).

Now let's connect load to this source. For simplicity, we will connect a resistor with resistance $ R_{in} $. Hence, the input impedance of this load is equal to $ R_{in} $. When we plot the I-V characteristics of the load with the source, the intersection of the two lines is the operating point.
Here we can see that once the load is connected to the source, the output voltage is no longer 9V; rather it is given by the operating point. The example drawn above shows the 9V battery having an output resistance of 1.5Ω and the load having an input resistance of 3Ω. If you use voltage divider relations to calculate the voltage being applied across the load, and the current flowing through it, you will find it to be 6V and 2Ω, respectively, as given by the operating point graphically. This shows us that even though the 9V battery outputs 9V when there's no current flowing, once we apply the load, the output voltage drops down to 6V to account for the increased current flow.
What would have happened if the load resistance were very high? Think about how the change in slope of the I-V curve for the load would affect the operating point.
Principle for loading circuits
After observing the previous example, you can see that loading a source where the input impedance of the load is similar in magnitude to the output impedance of the source causes the output voltage to drop. How can you load a source such that you maintain the output voltage?
If $ Z_{in} >> Z_{out} $ (input impedance of load >> output impedance of source), then the source can output close enough to it's open circuit voltage that we can ignore the changes induced by the load. One way to think about it is that if the input impedance of the load is very high compared to the output impedance of the source, then it's not going to draw much current from the source, and the voltage at the connecting point will be maintained. This is a good principle to follow when connecting different components together.
Practice examples
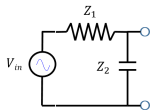
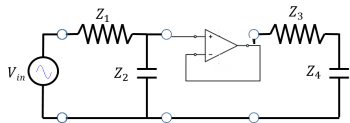
1. What is the output impedance $ Z_{out} $ of the following circuit? We want to connect another circuit to the blue nodes.
Solution: When finding the output impedance, we "look into" the blue output nodes of the circuit. Remember from the I-V curve shown previously, that $ Z_{out} = {V_{oc} \over I_{sc}} $, where $ V_{oc} $ is the open-circuit voltage (when the blue nodes are left open, $ V_{oc}=V_{in}{Z_2 \over Z_1 + Z_2} $) and $ I_{sc} $ is the short-circuit current (when the blue nodes are shorted, $ I_{sc}={V_{in} \over Z_1} $). In other words, the output impedance is similar to the Thevenin equivalent resistance. A short-cut way to find $ Z_{out} $ is to replace the voltage source with a wire and find the equivalent resistance or impedance. Here, if we replace the voltage source with a wire, the circuit looks like a resistor and capacitor in parallel, where $ Z_{out} = {Z_1 Z_2 \over Z_1 + Z_2} $.
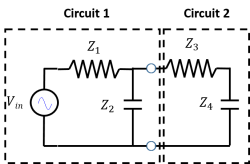
2. If we want to connect another low pass filter (Circuit 2) in series with the circuit from Question 1 (Circuit 1), what criterion must hold for us to ignore the loading effects of the second circuit? Write your answer in terms of $ Z_1, Z_2, Z_3, Z_4 $.
Solution: We know that for a load to be ignored, we need $ Z_{out} << Z_{in} $. Since we already found $ Z_{out} $ in Question 1, we now need to find $ Z_{in} $. Looking into the nodes of Circuit 2, it looks like a resistor and capacitor in series. There are no voltage sources to replace with wires here, we just have an open circuit with a resistor connected to a capacitor. Thus, $ Z_{in} = Z_3 + Z_4 $. Substituting for $ Z_{out} $ and $ Z_{in} $, the criterion for us to ignore the loading effects of Circuit 2 is if: $ {Z_1 Z_2 \over Z_1 + Z_2} << Z_3 + Z_4 $.
3. If we find that the criterion from Question 2 does not hold true, and Circuit 2 is loading Circuit 1, what can we put in between the two circuits to isolate their effects?
Solution: A buffer, consisting of an op-amp. We model an op-amp as having very low or negligible output impedance, and very high or infinite input impedance. Thus it can buffer the effects between two circuits as shown below.