Impedance Analysis
Overview of impedances
When a circuit contains capacitors and/or inductors, the behavior of the circuit can change with time. Furthermore, often while using these components, we are interested in time-varying input signals, such as a sinusoidal voltage input. Since the current-voltage relationships for capacitors and inductors involve derivatives or integrals, analyzing such circuits often involve differential equations. To simplify our calculations, we can perform the steady-state analysis of circuits with time-varying signals using the frequency domain instead of the time domain. For example, a sine wave constantly varies over time, but only contains one constant frequency. Here we will discuss how to approach circuits using this mind set.
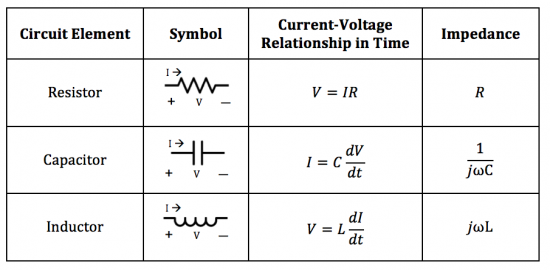
For analyzing the frequency response of circuits with various components, it is convenient to think of a generalized form of resistance, or opposition to current flow, known as impedance ($ Z $). Clearly, we know that a resistor's resistance to current flow is known by its resistance. Although capacitors and inductors don't technically have a "resistance" value, they do resist current flow in their own ways and we can call those their respective impedances. Thus, Ohm's law applies not only to resistances, but to impedances as well:
| $ V = I Z $ |
where $ V $ is the voltage drop across the components of interest, $ I $ is the current, and $ Z $ is the impedance of those components.
The table below indicates the impedance values for different circuit elements. Here, $ j $ is the imaginary number and $ \omega $ is frequency in units of radians. Recall that $ \omega = 2 \pi f $, where $ f $ is frequency in units of Hz.
Derivation of impedance
Below is a short demonstration of how we can derive the impedances for the circuit elements listed above. Let's use the capacitor as an example. Since we are interested in transient (time varying) signals, we will let voltage $ V $ be a time varying signal $ Ae^{j \omega t}. $ (Click here for a refresher on complex numbers.)
- Since we know that $ I = C {dV\over dt} $, we can take the derivative of V and plug it in:
- $ I = C A j \omega e^{j \omega t} $
- With some reorganizing, we can see that $ I = j \omega C V $
- To get it into the form $ V = I Z $,
- $ Z = {1\over j \omega C} $
This impedance value follows what we already know about capacitors--that they act as an open circuit with a constant DC voltage ($ Z \rarr \infin $ when $ \omega = 0 $, also $ I=0 $ because $ {dV\over dt}=0 $). At very high frequencies, as $ \omega \rarr \infin $, the capacitor acts as a short circuit, like a wire without resistance ($ Z \rarr 0 $).
The same exercise can be done for the inductor. It will be left as an exercise for the reader.
Impedances in series and in parallell
When combining the effect of multiple circuit components in series or parallel, their impedances can be treated as resistances. Thus, for elements in series, their impedances add. Meanwhile, for elements in parallel, the inverses of their impedances add. This is summarized in the following table.
Example circuit problem
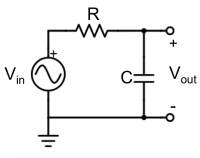
Find $ {V_{out} \over V_{in}} $ for the following RC circuit.
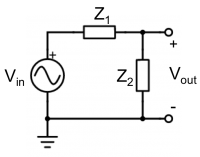
We can convert the circuit elements to look at their impedances, as in the diagram on the right, where the resistor has impedance $ Z_1 = R $ and the capacitor has impedance $ Z_2 = {1 \over j \omega C} $
We can see that this circuit is a voltage divider, where
- $ V_{out} = V_{in} {Z_2 \over Z_1 + Z_2} $
- Substituting back the impedance values,
- $ V_{out} = V_{in} {{1 \over j \omega C} \over R + {1 \over j \omega C}} $
- $ {V_{out} \over V_{in}} = {1 \over 1 + j \omega RC} $
We call this type of filter a low-pass filter, because at low frequencies ($ \omega $ small), the output voltage is very close to the input voltage. In other words, at low frequencies, the circuit passes the input voltage to the output. However, at high frequencies ($ \omega $ large), the output voltage is very small compared to the input voltage. Thus, at high frequencies, the circuit does not pass the input voltage to the output; rather, the circuit filters out or blocks the input signal from the output. We will define how high is a high frequency and how low is a low frequency in the Bode plots page.
(If you've forgotten about voltage dividers, please visit this page and/or this video.)