20.109(S21):M1D7
Contents
Introduction:Analyze ligand titration curves
"Each protein in a cell collides with a tremendous variety of other molecules every second, but the great majority of these interactions are fleeting and have no functional consequences. However, in a small minority of these collisions, a more persistent interaction occurs between the protein and its ligand, docking the two into a precise relative orientation. This complex may stay assembled anywhere from seconds to days and perform a variety of functions: catalysis of a chemical reaction, construction of an intracellular structure or compartment, or transmission of signaling information from the environment or between intracellular compartments."
Excerpt from Quantitative Fundamentals of Molecular and Cellular Bioengineering by K. Dane Wittrup, , Bruce Tidor, , Benjamin J. Hackel, , and Casim A. Sarkar. MIT Press, 2020.
How do we measure non-covalent binding between two molecules? The antigen, lysozyme (L), and antibody (Ab) form a complex (C), which can be written
$ L + Ab \rightleftharpoons\ C $
At equilibrium, the rates of the forward reaction (rate constant = $ k_f $) and reverse reaction (rate constant = $ k_r $) must be equivalent. Solving this equivalence yields an equilibrium dissociation constant $ K_d $, which may be defined either as $ k_r/k_f $, or as $ [Ab][L]/[C] $, where brackets indicate the molar concentration of a species.
Meanwhile, the fraction of antibody that are bound to antigen at equilibrium, often called y or θ, is $ C/Ab_{TOT} $, where $ Ab_{TOT} $ indicates total (both bound and unbound) receptors. Note that the position of the equilibrium (i.e., y) depends on the starting concentrations of the reactants; however, $ K_d $ is always the same value. The total number of antibody $ Ab_{TOT} $= [C] (L-bound Ab) + [Ab] (unbound Ab).
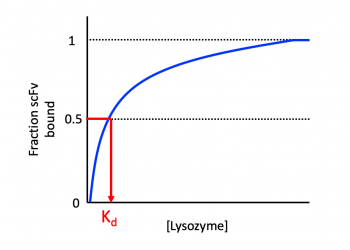
$ \qquad y = {[C] \over Ab_{TOT}} \qquad = \qquad {[C] \over [C] + [Ab]} \qquad = \qquad {[L] \over [L] + [K_d]} \qquad $
where the right-hand equation was derived by algebraic substitution. We can consider the relationship between the concentration of L and $ K_d $.
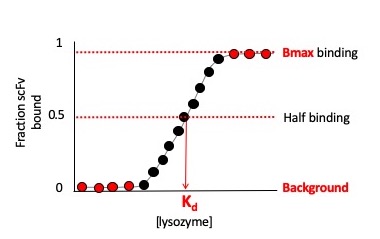
- If the antigen concentration [L] is in excess of the concentration of the antibody, [L] may be approximated as a constant, L, for any given equilibrium. So restate that when L>>$ K_d $, then y~1. The binding fraction is constant. The scFvs are saturated with lysozyme.
- If the antigen concentration [L] is equal to $ K_d $ then y=0.5 and this makes measuring apparent $ K_d $ easy. When 50% scFv are bound by lysozyme, the lysozyme concentration equals $ K_d $.
- If the antigen concentration [L] is much lower than $ K_d $ or [L]<<$ K_d $, then y~L/$ K_d $ and the binding fraction is directly proportional to L. The scFv bound are directly proportional to lysozyme concentration.
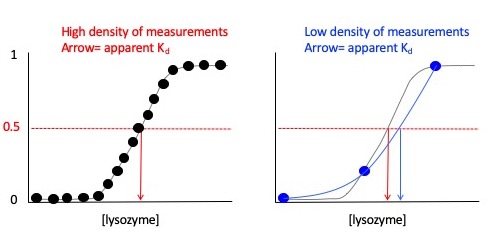
One final note, it's essential to an accurate $ K_d $ measurement that the experiment collect data points around the expected $ K_d $ and that a sufficient number of data points are collected. See the illustration below for why this is critical. To determine how many data points and what range of data points constitutes "accurate" usually required multiple experiments or prior knowledge of the bimolecular interaction you are studying.
Protocols
Motivation: To calculate the apparent $ K_d $ from our lysozyme titration experiments we will analyze the flow cytometry scatterplot data collected from the Accuri C6.
Part 1: Analyze flow cytometry scatterplots using FlowJo and generate Median Fluorescent Intensity (MFI) table
Today, we will be analyzing the flow cytometry data that we collected last lab class in order to assess the binding of your mutant scFv clones to lysozyme as compared to the parental scFv Lyso_scFv_6. On M1D5, you compared the sequences of two different mutant clones to the parental scFv DNA. This parental clone is reported to have a $ K_d $ of of 6 nM for binding to lysozyme. To assess differences in binding affinity between our mutants and the parental clone we will calculate and compare the apparent $ K_d $ of two mutants and the parental clone. Download FlowJo on to your computer and activate free 30-day trial
- Go to https://www.flowjo.com/solutions/flowjo/free-trial and click “Download”. Complete the software download instructions to install FlowJo v10.7 for your system (Mac or Windows).
- Once the software installation has finished, open the program and locate your computer’s hardware ID number in the license pop-up window. Complete the form using your email and ID number at the above link. If the license pop-up window does not automatically appear with your ID number, instructions to find the number through FlowJo are listed here: https://docs.flowjo.com/flowjo/faq/general-faq/locating-hwa/.
- Use the serial number sent to your email to activate your 30-day free trial.
Analyze scFv Flow Cytometry Titration Samples in FlowJo
- Access the flow cytometry data here. You and your team mate(s) will analyze the lysozyme titration data for the two clones you analyzed on "sequencing analysis day" or M1D5. You will also analyze the parental lysozyme titration data for comparison.
- All experiments are named by clone and have ten titrations. The number on the files correlates to the lysozyme concentration according to the following table:
| Titration number | Lysozyme concentration |
| 1 | 1000nM |
| 2 | 316nM |
| 3 | 100nM |
| 4 | 31.6nM |
| 5 | 10nM |
| 6 | 3.16nM |
| 7 | 1nM |
| 8 | 0.316nM |
| 9 | no lysozyme, secondary alone |
| 10 | no lysozyme, no secondary |
- When you have activated your trial, a blank workspace should have opened up in FlowJo. If not, open the FlowJo_v10.7 program and create a new workspace by clicking the “new” button.
- Add all of the sample files to your workspace (FlowJo Tab --> Add samples)
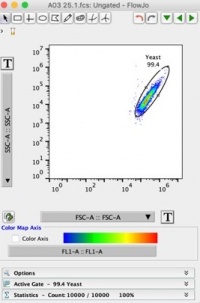
- Click on the first sample to open FSC-A vs. SSC-A plot. Change the axis to log scale by pressing the large [T] buttons by the axis labels. Use the oval gating tool at the top to select yeast cells (and exclude extraneous particles). Label this population as “yeast”. Your plot should look like Figure 1 below:
- Close the graph window and go back to the main workspace page and click on now gated “yeast” population below the first sample. This will open up a new graph with only the gated cells.
- We will now change our axis on the yeast scatterplot to analyze the data based on the fluorescence markers used in the secondary staining. Change the x-axis of the plot from “FSC-A::FSC-A” to “FL1-A::FL1-A” and the y-axis of the plot from “SSC-A::SSC-A” to “FL4-A::FL4-A”.
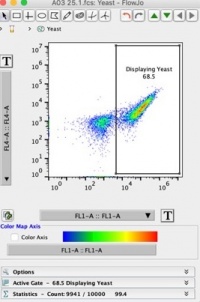
- The FL1-A channel and x-axis will measure the fluorescence intensity of the AF488 marker on our cells. Thus, dots farther to the right on the x axis represent cells that displayed more scFv on their surface.
- The FL4-A channel and y-axis will measure the fluorescence intensity of the AF647 marker on our cells. Thus, dots higher on the y axis represent cells with scFvs that bound lysozyme.
- We will now set two gates: yeast that displayed scFvs and yeast that did not display scFv. Despite the induction with galactose media not all yeast cells will display scFv on their surface (ex. Dead cells, budding cells). We want to analyze only the cells that displayed scFvs on their surface (right population.)
- Use the rectangle gating tool at the top to make a “displaying yeast” population. Your plot should look like Figure 2 below:
- We will now add statistics to our graph to obtain the Median Fluorescence Intensity of the y-axis AF647 binding signal. Under the “Edit” tab, choose “Add a Statistic”. A pop-up menu will appear.
- Choose the “displaying yeast” as your population drop-down option.
- Choose “Median” in the statistic options menu on the left.
- Choose “FL4-A::FL4-A” as the statistic options menu on the left and select “Add” at the bottom.
- Close the graph and return to the workspace screen. Your first sample should now have the following sub-populations listed below:
- We now need to copy all of the sub-populations and statistics below the first sample to the other samples in our workspace. Select all of the subpopulations and statistics (select top, hold shift key, select bottom) and copy them (via ctrl+c, or copy in edit tab). Select the remaining samples and paste the subpopulations and statistics. All of the samples should now have the same five sub-populations and statistics.
- At this point, we need to check our control samples to ensure our gates are set correctly. We want to make sure that our "displaying yeast" gate excludes cells that do not display scFvs but may be slightly sticky to AF488. Make sure to check your controls. We want to set our gate to include minimal sticky cells.
- Next, we will export the statistics in a table. Under the “FlowJo” tab, select “Table Editor”
- Under the “Edit” tab in the Table Editor pop up window, select “Add Column”.
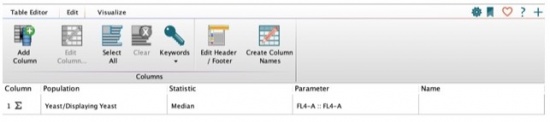
- Add the two statistics to your table that you just added to your samples in your workspace using the same populations (displaying yeast), statistics (Median), and parameter (FL4-A::FL4-A). Your window should look like the following:
- Return to the “Table Editor” tab and “Create Table” by pressing the gear symbol.
- Save the table as an excel file for further analysis. These values are critical for next steps.
In your laboratory notebook, complete the following:
- Note the mutant number (eg. H1) and annotate the amino acid mutations associated with each mutant as "Heavy Chain Gly200Cys." The number between the parental amino acid and the mutant amino acid should represent the amino acid number in the scFv feature translation.
- Copy and paste the MFI values for the parental control, Mutant 1 and Mutant 2 your team analyzed in your notebook and on the discussion tab of this wiki page.
- What can you infer from the MFI values of your mutants vs. parental? Are the MFIs higher or lower for a given lysozyme concentration?
- What can you infer from the scatterplots of the titration experiments? Do you think your mutant was a good binder compared to the parental?
Part 2: Plot logarithmic titration binding curves and calculate apparent $ K_d $ via Matlab
Motivation: To calculate the apparent $ K_d $ from the median fluorescent intensity of our flow cytometry titration we will use Matlab to carry out the statistical analysis and fit a curve to the data.
The Matlab code will fit your titration curves for your scFv binding to lysozyme as measured via flow cytometry. The Inputs required are concentration of lysozyme and corresponding fluorescence values for controls and mutant clones at those concentrations. To determine the apparent $ K_d $, we will use Matlab to calculate three values from our median fluorescent intensity data: Bmax, $ K_d $ and background signal.The output of this code will be a plot with titration curves and Kd values
You will need to either run Matlab software on your computer, or by using the online Matlab server found here: Matlab Online. Please note that you will need to make an account with Matlab using your MIT email address and use the MIT software license for free access. Instructions below are for Matlab online.
- Copy the Matlab code here: Solve for Kd (right click to download file.) This code is also available in your dropbox class data folder.
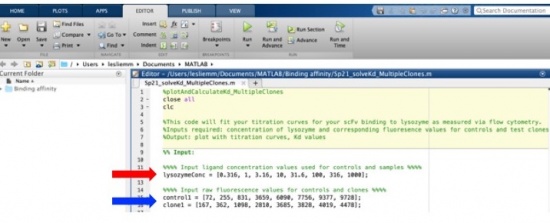
- Open the code in Matlab and review the first few lines in the editor window.
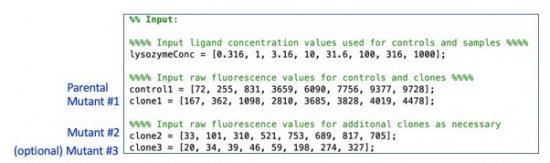
- Check that the lysozyme concentration listed are accurate to the concentrations used in your experiment. (red arrow in figure above)
- Next input the MFI values you calculated from the parental clone next to the text of control 1. Separate the values by commas and input the values from lowest lysozyme concentration to highest. (Blue arrow in figure above)
- Repeat this process for one or both of the mutants your team analyzed.
- Hit the green run arrow at the top of the editor window.
- The code will calculate the maximal binding (Bmax), the equilibrium binding constant ($ K_d $), and background signal from the input data points. It will use these values to plot a logarithmic binding curve and include the apparent $ K_d $ on this plot.
- Within a few seconds a plot should pop up.
- It's your choice if you'd like to include a second and third mutant clone in your analysis. If so, use your classmates MFI values from the discussion tab of this page to carry out this analysis again.
In your laboratory notebook, complete the following:
- Report the $ K_d $ of each of the clones from your graph.
- Which mutant (or parental) has the highest $ K_d $?
- Which mutant (or parental) has the lowest $ K_d $?
- Rank the scFvs in order from weakest to strongest lysozyme binders.
- Can you make connections between the type of amino acid mutations of your mutant and the strength of binding to lysozyme?
Reagents list
FlowJo software
Matlab software
Next day: Perform protein purification protocol