Difference between revisions of "Electronics Mini-Lab"
(→Build the circuit) |
|||
| (584 intermediate revisions by 7 users not shown) | |||
| Line 2: | Line 2: | ||
[[Category:Electronics]] | [[Category:Electronics]] | ||
{{Template:20.309}} | {{Template:20.309}} | ||
| + | |||
| + | [[Image:Resistor Bug.jpg|right|300 px|thumb|Photo by Brendan Dolan-Gavitt]] | ||
==Overview== | ==Overview== | ||
| − | During the next lab exercise on measuring DNA melting curves, you will | + | During the next lab exercise on measuring DNA melting curves, you will build and debug several electronic circuits. This bootcamp will introduce you to the electronic components and test equipment you will use. A short answer-book style writeup is required. Your writeup should include the practice problems and any '''bolded questions''' asked throughout the lab instructions. Don't forget the basics: report measurements with an appropriate number of significant figures, units, and uncertainty. Label plot axes. |
| + | |||
| + | This bootcamp requires an understanding of basic circuits. If you need to review circuit concepts, start with the [[Electronics Primer]] page. If you have a lot of experience with electronics, ask one of the instructors about doing a stimulating mini-project instead of the mini-lab assignment. | ||
| + | |||
| + | ==Problems== | ||
| + | ====Question 1==== | ||
| + | Consider the following circuit composed of a network of resistors: | ||
| + | [[Image: Circuit1.png|center|250px|thumb]] | ||
| + | |||
| + | '''a)''' Combining resistance values in parallel and in series, draw a simplified version of the circuit containing the given voltage source (10V) and one equivalent resistor. Label the equivalent resistance value. | ||
| + | |||
| + | '''b)''' Find the voltage values for the nodes <math>V_A</math> and <math>V_B</math> in the above diagram. | ||
| + | |||
| + | ====Question 2==== | ||
| + | Referring to the circuit shown below, what value of <math>R_L</math> (in terms of <math>R_1</math> and <math>R_2</math>) will result in the maximum power being dissipated in the load? | ||
| + | |||
| + | Hint: this is much easier to do if you first remove the load, and calculate the equivalent Thevenin output resistance <math>R_T</math> of the divider looking into the node labeled <math>V_{out}</math>. Then express <math>R_L</math> for maximal power transfer in terms of <math>R_T</math>. | ||
| + | |||
| + | [[Image: VoltageDivider.jpg|center|200px|thumb|A voltage divider formed by <math>R_1</math> and <math>R_2</math> driving a resistive load <math>R_L</math>.]] | ||
| + | |||
| + | |||
| + | ====Question 3==== | ||
| + | In the following circuit, R = 10 kΩ and C = 10 nF. | ||
| + | [[Image: Filter1.jpg|center|220px|thumb]] | ||
| + | |||
| + | '''a)''' Find the transfer function <math>{V_{out} \over V_{in}}</math>. | ||
| + | |||
| + | '''b)''' What type of filter is this? Justify your answer. | ||
| + | |||
| + | '''c)''' What is the cutoff frequency of this filter? Write your answer in units of Hz. Remember that <math>\omega = 2 \pi f </math>. | ||
| + | |||
| + | Note: You may find the pages on [[Impedance Analysis]] and [[Bode plots| Transfer Functions and Bode Plots]] helpful for this problem. | ||
| + | |||
| + | ==Lab Exercises== | ||
| + | ===Voltage divider=== | ||
| + | [[Image:VdividerSchematic_idealsymbol.png|right|250px|thumb|Schematic diagram of voltage divider circuit.]] | ||
| + | |||
| + | In the first hands-on part of the bootcamp, you will analyze and build a voltage divider. The divider circuit comprises two resistors and a voltage source, as shown in the schematic diagram. You will select the values for ''R<sub>1</sub>'' and ''R<sub>2</sub>''. | ||
| + | |||
| + | ====Before you build==== | ||
| + | Choose any two resistor values you like, but there are a few practical constraints. The resistors in the lab range in value from 1 Ω to 10 MΩ. Within that range, manufacturers only produce certain standard values. Check the supply bins or [http://ecee.colorado.edu/~mcclurel/resistorsandcaps.pdf this table] to see which values are available. | ||
| + | |||
| + | Resistors convert electric power to heat. Since the ideal circuit model does not include heat energy, ideal resistors have the effect of making power disappear from a circuit. Of course, energy is conserved in a real circuit. The energy is converted to a form that is extrinsic to the ideal circuit model. | ||
| + | |||
| + | The fact that energy disappears from a circuit model doesn't mean that you can ignore it. Power dissipation in resistors increases in proportion to resistance and the square of current, <math>P=I^2R</math>. Physical resistors must be able to shed their heat to the environment or else they tend to get very hot and fail. A noxious puff of smoke frequently accompanies failure. Even if a component operated at an excessive power level does not vaporize, it may no longer behave as specified. The maximum power rating of the resistors in the lab is ¼ Watt. Ensure that the power dissipated by ''R<sub>1</sub>'' and ''R<sub>2</sub>'' does not exceed the maximum rating for ''V<sub>in</sub>'' values in the range of 0-15 V. | ||
| + | |||
| + | You will use an oscilloscope and a volt meter to measure voltages in the circuit. The oscilloscope has an input impedance of 1 MΩ. Connecting the oscilloscope probe to a node of the circuit is equivalent to placing a 1 MΩ resistor between that node and ground. In circuits that use very large resistors, the current flowing into the oscilloscope can significantly distort measurements. | ||
| + | |||
| + | Before building the divider circuit: | ||
| + | |||
| + | # '''Record the values you selected for R<sub>1</sub> and R<sub>2</sub>.''' | ||
| + | # '''Find the gain of the circuit, <math>^{V_{out}}/_{V_{in}}</math>''' | ||
| + | # '''Plot an ''I-V'' curve with ''I'' on the vertical axis and ''V<sub>in</sub>'' on the horizontal axis, over the range 0 V < ''V<sub>in</sub>'' < 15 V.''' | ||
| + | #* A hand-drawn plot is fine. | ||
| + | # '''What is the maximum power dissipated in each resistor between 0 V < ''V<sub>in</sub>'' < 15 V?''' | ||
| + | |||
| + | ====Another practical issue: tolerance==== | ||
| + | [[Image:Museum_of_tolerance.jpg|right|thumb|The [http://www.museumoftolerance.com Museum of Tolerance] in Los Angeles, California contains many exhibits about the concept of tolerance.]] | ||
| + | |||
| + | It's easy enough to write down an exact value for a resistor like 15 kΩ or e<sup>π</sup> Ω and analyze a circuit model that contains such a component. But fabricating a 15 kΩ or e<sup>π</sup> Ω resistor is another matter. It is not possible to realize physical components with infinite precision. The values you specify on paper are called nominal values. Nominal means: "stated or expressed but not necessarily corresponding exactly to the real value."<ref>http://www.merriam-webster.com/dictionary/nominal</ref> When you go to build the circuit, the actual value of the resistors you use will be somewhat different than the nominal values you used to analyze the circuit. | ||
| + | |||
| + | To account for the difference between the nominal and actual values of a component, the manufacturer guarantees that the actual value will differ from the nominal value by no more than a certain amount. Resistor tolerances are usually specified as a percent of nominal value. Some common resistor tolerances are 10%, 5%, 2.5%, and 1%. Even smaller tolerances are available from some manufacturers — down to 0.05& in some cases. The resistors in the lab are guaranteed by the manufacturer to be within 5% of the nominal value. | ||
| + | |||
| + | Because the actual values of the resistors differ from the nominal values, the power dissipation in ''R<sub>1</sub>'' and ''R<sub>2</sub>'' will under some circumstances be greater than what you computed using the nominal values. To be safe, the best thing to do is compute the power dissipated in both resistors under worst-case assumptions. | ||
| + | |||
| + | ====Measure the resistors with a digital multimeter==== | ||
| + | [[Image:ElectronicsModuleFig-MM.png|125 px|thumb|right|Digital multimeter with test leads configured for voltage or resistance measurement.]] | ||
| + | Go ahead and get the resistors for your circuit from the bins in the lab. | ||
| + | |||
| + | The value of each resistor is indicated by a set of color-coded bands on the component body. Through negligence or malice of last semester's scholars, components occasionally end up in the wrong bin. Ensure that you have the correct resistors by reading the color bands. Instructions for reading resistor markings are available at [http://en.wikipedia.org/wiki/Electronic_color_code this Wikipedia page]. | ||
| + | |||
| + | Measure the actual value of both resistors with a digital multimeter (DMM). DMMs are multifunction instruments that usually include functions for measuring voltage, current, and resistance. They connect to component terminals through a pair of test leads. DMMs measure resistance by applying a small voltage across the test leads and measuring the resulting current flow. To get an accurate measurement of a resistor, its leads must be isolated from other circuit elements. If the resistor leads are connected to other components, current flowing through other paths will distort the measurement. | ||
| + | |||
| + | # Plug two test leads into the DMM. | ||
| + | #* The black lead goes into the terminal labeled COM. | ||
| + | #* The red lead plugs into different terminals depending on the measurement you are making. For resistance measurements, use the '''V Ω''' terminal. The '''A''' terminal is for current measurements. | ||
| + | # Select the resistance mode, which is labeled with an Ω symbol. | ||
| + | # If you've inserted your resistors on the breadboard, remove them and connect the DMM leads to the resistor that you want to measure. | ||
| + | # '''Measure your resistors and record their actual values.''' | ||
| − | + | From this point on, use the actual value instead of the nominal value in your calculations. Using the actual value will reduce the error in results that depend on ''R<sub>1</sub>'' or ''R<sub>2</sub>''. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | == | + | ====Build the circuit==== |
| − | = | + | [[Image:Vdivider_Breadboard_zoom.png|right|thumb|An example voltage divider circuit implemented on a breadboard. Note that you don't need as many connections and can build the circuit however you choose.]] |
| − | [[Image: | + | [[Image:ElectronicsModuleFig-BB.png|right|thumb|Top view of a solderless electronic breadboard.]] |
| − | + | The next step is to build the divider circuit. If you have worked with electronic components before, you probably noticed that most of them look a little bit like bugs. They have a central body with some gangly legs sticking out, called leads. The leads carry current from the outside of a component to its innards where the magic happens. One of the first challenges facing an aspiring circuit maker is to properly connect all the bugs' legs whilst keeping the circuit robust and orderly. Solderless electronic breadboards are a convenient platform for building circuits that might require a lot of debugging or frequent reconfiguration. Breadboards are flexible and easy to use, but they have a few downsides. They have high interconnect capacitance and resistance. If you don't know why that's bad, pay closer attention in lecture. | |
| − | + | Before you go on, gather the items that you will need: | |
| − | + | * solderless electronic breadboard, | |
| − | + | * lengths of different colored wire to make jump wires, | |
| + | * wire strippers (located in the lab station tool drawers). | ||
| + | The image on the right shows an example of solderless electronic breadboard. The breadboard has a large number of square holes in it called ''tie points''. A single wire or component lead fits into each tie point. Spring-loaded contacts inside each tie point hold leads in place and provide electrical connections. | ||
| − | + | Sets of tie points are electrically connected to each other in a pattern that allows just about any circuit arrangement to be realized on the breadboard. The two central grids of tie points separated by a notch are called the field. Each row of tie points in the field is called a terminal strip. Rows of terminal strips are numbered. Columns are designated by a letter. Within a terminal strip, the five tie points A-E are connected, and tie points F-J are connected. Points A-E are not connected to points F-J. Connections between component leads are made by running jump wires between tie points that are connected to each lead, as shown in the image above on the right. | |
| − | + | The long lines of tie points to the left, right, and above the field are called bus strips. Bus strips are highlighted by red and blue lines. All of the tie points in a bus strip are connected together. Because most circuits have a lot of power and ground connections, the bus strips are almost always connected to the power supply. Using the bus strips as a power distribution network makes it easy to connect any terminal strip to power or ground with a short jump wire. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | to | + | |
| − | + | If you are unsure whether two holes on the breadboard are connected, insert short wires in the holes. Use the resistance or continuity features of the DMM to check if they are connected. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | # Mount R<sub>1</sub> on the breadboard by bending its leads at a 90 degree angle and trimming them to about half an inch long. Press the leads into the breadboard. | |
| + | # Mount R<sub>2</sub> so that one of its leads is in the same terminal strip as one of the leads from R<sub>1</sub>. This will create an electrical connection between the two resistors. | ||
| + | ====Connect the power supply==== | ||
| + | [[Image:ElectronicsModuleFig-PS.jpg|right|thumb|Triple-output DC power supply.]] | ||
| − | + | Now it's time to complete the circuit by connecting a voltage source. You will use a laboratory power supply to drive your circuit. The lab supply has three separate DC outputs called '''CH1''', '''CH2''', and '''CH3'''. Each supply has a '''+''' and '''-''' terminal, from which motivated electrons begin and end their journeys. <ref>Don't read this if you think you understand circuits. The electrons begin their journey at the minus terminal; however, positive current is defined to flow from plus to minus. It's all <a href="http://www.allaboutcircuits.com/vol_1/chpt_1/7.html">Benjamin Franklin's fault</a>.</ref> The '''CH1''' and '''CH2''' outputs are adjustable. The '''CH3''' output always produces 5 volts with a current limit of 3 amps. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | When you turn the power supply on, all three of the outputs will be disabled (which is a rather sensible way of doing things). Press the '''OUTPUT''' button to enable all three supplies. Press '''OUTPUT''' again to disable all three supplies. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | (a) | + | |
| − | the | + | |
| − | + | ||
| − | + | ||
| − | + | Four dials on the front of the supply set the current and voltage limits for each of the two supplies from 0-20V and 0-3A. At all times, each adjustable supply will be either current or voltage limited. Multicolor LEDs indicate which limit is currently in effect: green for voltage-limited and red for current-limited. When the supply is disabled, the numeric displays will show the values of the limit settings. When the supply is in operation, the displays show the actual current and voltage values for each supply. | |
| + | Two pushbuttons near the middle of the the lab supply control panel configure the interconnection of '''CH1''' and '''CH2'''. There are 3 possible settings: independent, series, or parallel. In independent mode, '''CH1''' and '''CH2''' are not connected together. The two sets of voltage and current dials operate independently. In series mode, the plus terminal of '''CH2''' supply is internally connected to the minus terminal of '''CH1'''. Both supplies operate with the same voltage limit. The current limits are independent. This provides a ''split supply'' with equal positive and negative voltages relative to the common terminal. In parallel mode, the '''+''' terminals of '''CH1''' and '''CH2''' are connected together, as are the '''-''' terminals. Parallel configuration allows a maximum possible current of 6 amps — 3 amps from each of the supplies. | ||
| − | '' | + | The post labeled "GND" in green letters is connected to ''earth ground''. Earth ground is a wire that runs through the third prong of the electrical plug to a post driven deep into the ground somewhere near Building 16. Earth ground is not needed for this lab. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | In this part of the lab, you will use a 15 volt, split supply. Configure the lab supply in series mode with a voltage of 15 V and a current limit of about 0.1 amps on '''CH1''' and '''CH2'''. | |
| − | + | The breadboard has four colored post terminals at the top right to facilitate power supply connections. These are called banana post terminals. Each post terminal accepts a banana connector inserted at the top and a bare wire at the base. The banana terminals are not connected to any of the tie points, so it is necessary to run wires from the post terminals to tie points on the bus strips. Wires connected to the post should pass through the hole through the base of the post. Be sure that only bare wire touches the terminal. Insulation under the screw terminal may cause an intermittent connection. Secure the wire by tightening the colored plastic nut (onto bare wire, not insulation plastic sleeve). | |
| − | + | Use jump wires to connect the power post terminals to the bus strips on the breadboard. Hook up the power as shown in the picture above (note that the circuit shown is not yet complete, however). Power the voltage divider circuit by connecting it to the +15 V bus strip and ground. | |
| + | # Use the cutting jaws of the wire stripper to trim the resistor leads so that the component bodies will be close to the board. | ||
| + | #* In addition to being untidy, leads that are too long may make unintentional contact with the metal under the breadboard. | ||
| + | #* Don't cut the leads too short either, or they may not make good contact with the tie point. | ||
| + | # Mount the resistors by pressing their leads into tie points in the field. | ||
| + | # Run jump wires to connect the divider to the power and ground bus strips. | ||
| + | #* Keep your wiring neat, close to the board, and easy to follow. A good way to do this is to route wires horizontally or vertically, making right-angle bends to change directions. | ||
| + | #* Use the right length of wire. The right length of wire is the shortest length of wire that satisfies the previous guideline. | ||
| + | #* Use the bus strips to distribute power supplies and ground as described in the text above. | ||
| + | Use a cable with banana connectors on both ends to connect the power supply to the posts. You can find banana cables hanging on the cable rake near the time travel poster. Refer back to left side of the lab map in [[Optics_Bootcamp#Orientation|lab orientation]] if you need to. Convention is to use black cables and connectors and blue bus strips for ground. Red bus strips are almost always used for power supplies. | ||
| − | + | The exposed metal screws on the bottom of the banana connectors (on the back side of the breadboard) can short to the metal optical table. Cover them with electrical tape to prevent a calamity. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | ====Measure voltage ''V<sub>out</sub>''==== |
| + | [[Image:VoltageMeasurementZoomText.png|250 px|thumb|Test leads in parallel with ''R<sub>2</sub>''.]] | ||
| + | The DMM has modes for measuring DC and AC voltages. In DC mode, the meter reads the average value of the test signal. In AC mode, the meter reads the root-mean-square value of a time varying signal. In this lab you will use DC mode, which is labeled with a solid line above a dashed line. | ||
| − | + | #Switch the DMM to DC voltage mode and connect the DMM test leads. Insert the black lead into the receptacle marked '''COM''' and the red lead in '''VΩ'''. | |
| + | #Connect the test leads across the terminals of ''R<sub>2</sub>''. | ||
| + | #'''Record the voltage shown on the DMM for each input voltage ''V<sub>in</sub>'' = 0, 2.5, 5, 10 and 15 V.''' Hint: You can make the +15 V bus strip whatever voltage you want simply by adjusting the voltage at the power supply. | ||
| − | + | The DMM has a very high input impedance. We can simulate the effect of an inferior meter with lower input impedance by adding a 1 kΩ resistor in parallel with ''R<sub>2</sub>''. | |
| − | + | ||
| − | + | #'''Add the 1 kΩ resistor in parallel with ''R<sub>2</sub>'' and measure the voltage across ''R<sub>2</sub>''. By what percentage did the measurement change?''' | |
| + | #Remove the 1 kΩ resistor and the DMM from the circuit. | ||
| − | + | ====Measure current ''I''==== | |
| − | + | [[Image:CurrentMeasurementZoomText.png|250 px|thumb|right|DMM test leads connected in series with ''R<sub>2</sub>''.]] | |
| − | + | In order to measure current, you must move the red test lead from the '''VΩ''' receptacle on the DMM to the '''A''' receptacle. The reason for the change is that there is a fundamental difference between measuring voltage and current. Voltage is a measure of potential; current is a measure of flow. To make an accurate voltage measurement, the meter should have very high input impedance. High input impedance in a voltage measurement ensures that only a small percentage of the current flowing in the circuit goes through the meter. Measuring current essentially requires counting the number of electrons that flow past a certain point in a given time, so the opposite is true. To get a good count, all of the current must flow through the meter. Making a good current measurement requires a meter with very low input impedance. In addition, you must place the meter in series with the current you want to measure so that all of the current flows through the meter. | |
| − | + | * ''Note:'' In the 20.309 lab, the Fluke 115 DMMs can accurately measure a few milliamps of current, while the 111 models should not be trusted at very low current levels. Click these links for full documentation for the (discontinued) [http://www.fluke.com/fluke/m2en/digital-multimeters/Fluke-110.htm?PID=55988 Fluke 111] and [http://www.fluke.com/fluke/m2en/digital-multimeters/Fluke-115.htm?PID=55993 Fluke 115] multimeters. | |
| − | + | * For this section of the electronics mini-lab, feel free to swap R<sub>1</sub> and R<sub>2</sub> for smaller-value resistors, so the current flowing through R<sub>2</sub> is large enough to be measured by your Fluke 11x ammeter. Simply make a note of the new resistor values and justify your choice in your lab report. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | * | + | |
| − | + | # Switch the DMM to DC current mode and configure the leads for current measurement. | |
| + | #* Move the red lead to the receptacle marked '''A'''. | ||
| + | #* Positive current flows into the red lead and out of the black. | ||
| + | # Place the leads of the DMM in series with R<sub>2</sub> as show in the image at right. | ||
| + | # '''Record the current through the circuit at each input voltage ''V<sub>in</sub>'' = 0, 2.5, 5, 10 and 15 V''' | ||
| + | # '''Plot the measured ''I-V'' curve on the same set of axes as the calculated curve.''' | ||
| − | |||
| − | === | + | ===RC low-pass filter=== |
| − | + | [[Image:LowPassFilter.png|275 px|thumb|RC filter circuit schematic.]] | |
| − | + | In this part of the lab, you will replace R<sub>2</sub> with a capacitor. This will transform your humdrum voltage divider circuit into a spectacular low-pass filter. You will measure the time constant and frequency response of the filter circuit. Capacitors are available in the lab with a range of values from 0.01 - 0.1 uF. Check the supply bins to see what is available and choose a value for C<sub>1</sub>. | |
| − | + | # '''Choose a capacitor value and calculate the cutoff frequency of your filter.''' | |
| − | + | #* If the frequency is below 100 Hz or above 10 kHz, you might want to rethink your capacitor or resistor choice. Change either the resistor or capacitor to get a cutoff frequency in this range. | |
| − | + | # '''Draw a Bode plot of the filter response using straight line segments to approximate the transfer function.''' (For help with drawing Bode plots, visit the page on [[Bode plots]].) | |
| − | + | # Replace ''R<sub>2</sub>'' with a capacitor of the selected value. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[Image:Filter_Breadboard_Zoom.jpg|300 px|thumb|RC filter on a breadboard.]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | === | + | ====Replace the power supply with a function generator==== |
| − | + | [[Image:140127_FunctionGenerator.png|300 px|right|thumb|An SFG-2120 digital function generator.]] | |
| − | + | The behavior of ideal resistors is independent of frequency, so it was possible to measure the (frequency independent) transfer function of a voltage divider using the constant voltages produced by a lab power supply. Since the impedance of a capacitor varies in proportion to the inverse of signal frequency, it will be necessary to measure the response of the low-pass filter circuit over a range of frequencies. This requires a more sophisticated method of creating input voltages. Sine and square waves are especially useful for this task. In this part of the lab, you will also replace the power supply with a ''function generator'', which is a piece of equipment that can generate several kinds of periodic signals: sine, triangle, and square waves. The amplitude and frequency of the function generator's output are adjustable. | |
| − | + | ||
| − | + | ||
| − | + | There are several types of function generators in the lab. The digital function generators allow you to enter frequencies on a keypad. Press one of the unit keys (Hz, kHz or MHz) to complete your entry. Use the decade selector knob and frequency dial to set the frequency of the analog function generators. The output frequency is adjustable between about 0.01 Hz and 10 MHz. Amplitude ranges from 0.1 V to 10.0 V. | |
| − | # | + | # Disable the power supply and disconnect it from the circuit. |
| − | # | + | # Connect a function generator in place of the power supply. |
| − | # | + | #* Attach a BNC cable to the '''Output''' connector on the front right of the function generator. |
| − | # | + | #* This circuit is sensitive to the parasitic capacitance added to a circuit by multiple jump-wire to tie-point connections, so use a BNC to grabby clip adapter to connect directly to the left side of the resistor as shown in the picture. Remove the jump wires between there and the +15 V bus strip. |
| + | #* The connections can also be made using BNC to bare wire adapters found in the bins on the south wall. | ||
| + | #* The center conductor of the BNC cable is the positive signal lead; the outer conductor/shield is the ground signal lead. | ||
| + | # Turn on the function generator. | ||
| + | #* Set the frequency to 10 Hz. | ||
| + | #* Select a sine wave output. (Press the '''WAVE''' button on the digital function generators or use the waveform knob on the analog generators.) | ||
| − | + | ====Connect an oscilloscope==== | |
| + | [[Image:140127_Oscilloscope_LowPassRC.png|300 px|thumb|right|Digital oscilloscope.]] | ||
| − | + | Oscilloscopes provide a graphic display of time-varying voltage signals. In the most frequently used mode, the oscilloscope screen shows a plot of voltage on the vertical axis versus time on the horizontal axis. The oscilloscopes in the lab have two inputs. Either or both of the inputs may be plotted. Two knobs adjust the voltage and time scales so that it is possible to display a wide range of waveforms. The display also includes status indicators and configurable waveform measurements such as amplitude, frequency, and phase. | |
| − | + | ||
| − | + | Click these links for full documentation for the [http://www.tequipment.net/pdf/Rigol/DS1000E_DS1000D_series_manual.pdf Rigol DS1052e] and [http://micromir.ucoz.ru/Oscil/Atten/ADS1000_User_Manual.pdf ATTEN ADS1022c] oscilloscopes. | |
| − | + | ||
| − | [ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | # Get two oscilloscope probes from the cable rakes on the wall next to the time machine poster. |
| + | # Connect the oscilloscope to the circuit. '''CH2''' will monitor ''V<sub>in</sub>'', '''CH1''' ''V<sub>out</sub>''. | ||
| + | #* Connect the BNC connector of the first oscilloscope probe to the '''CH1''' oscilloscope input. Connect the probe to ''V<sub>out</sub>'', the top of the capacitor, using a small jump wire held in the retractable clip at the end. Connect the black alligator clip to ground, the bottom of the capacitor. '''CH1''' is thus in parallel with the capacitor. | ||
| + | #* Using a BNC T-connector, attach the other oscilloscope probe to the '''CH2''' input and to ''V<sub>in</sub>'' from the function generator. | ||
| + | # Set the oscilloscope vertical scale for each channel to 5 V per division. | ||
| + | #* The Rigol oscilloscopes have one knob that controls the vertical scale for both channels. Press one of the channel select buttons before you adjust the "vertical position" knob until the bottom-row display indicates "CH1 - 5.00V" and "CH2 - 5.00V". | ||
| + | #* The ATTEN oscilloscopes have a knob for each channel. Software menu functions still require you to press the button for the desired channel. | ||
| + | # Make sure the scope triggers on '''CH2''': | ||
| + | #* The oscilloscope begins recording and displaying the waveform when it is ''triggered''. There are several options to configure when the trigger occurs. One of the simplest modes causes a trigger when the input signal crosses a certain voltage level. | ||
| + | #* On both the Rigol and the ATTEN oscilloscopes, press the "menu" button of the right "Trigger" panel, and on the screen select "CH2" as the "Source". Adjust the trigger level by rotating the "Level" knob. | ||
| − | + | ====Measure and plot the transfer function==== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | # | + | # Set up the signal generator for 5 V peak-to-peak, sine wave output. |
| − | # | + | #* Select sine-wave mode using the mode buttons. |
| − | # | + | #* Set the peak-to-peak amplitude of the signal generator's output to 5 V using the "Ampl" tab on the function generator. |
| − | # | + | # Use the "Freq" tab on the signal generator to select a frequency of 10 Hz. |
| + | # Adjust the horizontal scale on the oscilloscope to display about 3 periods of the sine wave. | ||
| + | # Record the peak-to-peak amplitude of V<sub>out</sum> and V<sub>in</sub>. | ||
| + | #* The oscilloscope has a built-in feature for measuring peak-to-peak voltages that will make your life much easier. | ||
| + | #*# Press the "Measure" button in the "Menu" top panel | ||
| + | #*# Choose the channel of interest under "Source" | ||
| + | #*# Choose "Vp-p". | ||
| + | # Repeat the measurement of V<sub>out</sub> and V<sub>in</sub> at frequencies of 100 Hz, 1 KHz, 10 KHz, 100 KHz, 1 MHz, and several frequencies in the vicinity of the cutoff frequency. | ||
| + | # Make a Bode plot | ||
| + | #* '''Plot the measured values of <math>\frac{V_{out}}{V_{in}}</math> versus frequency on the same set of axes as your Bode plot. | ||
| − | === | + | ===Identify unknown filter circuits=== |
| − | + | In this part of the lab, you will measure the transfer function of four filter circuits made out of resistors and capacitors. The circuits will be hidden inside blue boxes marked A through D. Your goal is to figure out what type of circuit is inside of each "black box." | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | All of the boxes have two BNC connectors. You will use a function generator to drive sine waves of various frequencies into one connector and an oscilloscope to measure the resulting output on the other connector. Input and output are marked on the box. | |
| − | + | ||
| − | + | Measure each box at each decade of frequency between 10 Hz and 1 MHz. You may want to measure choose additional frequencies in transition regions. The transfer function consists of two plots: one that shows the magnitude of the output divided by the magnitude of the input as a function of frequency; and another that shows the phase difference between the input and the output. The former is the Bode gain plot like that for your RC filter. The latter is the Bode phase plot. From those plots, you can derive the topology of the circuits inside and determine the cutoff frequencies of each filter. | |
| − | + | # Use BNC cables to connect the function generator and oscilloscope to a box. | |
| − | a | + | # Set the scope to trigger from the input channel. |
| − | + | # Measure the input, output, and phase difference at a range of frequencies. | |
| − | and | + | #* Make sure to take enough measurements to completely identify the transfer function. |
| − | ''' | + | #* Take extra measurements in the vicinity of the cutoff frequency or frequencies. |
| − | and | + | # '''Generate the Bode gain plot and the Bode phase plot for each of the four black (blue) boxes: A through D.''' |
| − | + | # '''Draw the circuit inside each box.''' | |
| − | + | # Optional: '''In Matlab, use <tt>nlinfit</tt> to fit parameters of a transfer function for each circuit.''' | |
| − | + | ||
| − | + | ||
| − | |||
| − | === | + | ===Photodiode ''I-V'' curve=== |
| − | [[Image: | + | [[Image:PhotodiodeSchematic_v2.png|250 px|thumb|Photodiode measurement circuit schematic diagram. AC power supply symbol V<sub>1</sub> represents a function generator. Power supply to the ADS622 not shown.]] |
| − | In the | + | In this part of the lab, you will examine how light falling on a photodiode affects its ''I-V'' characteristic. You will use a function generator and an instrumentation amplifier to make simultaneous measurements of voltage across and current through the photodiode and plot an ''I-V'' curve on an oscilloscope. |
| − | + | ||
| − | + | In the preceding sections of this lab, you used an oscilloscope to plot voltage signals versus time. The oscilloscope also has an X-Y mode. In X-Y mode, the oscilloscope plots channel 1 on the horizontal axis versus channel 2 on the vertical axis. Using X-Y mode, it is possible to use an oscilloscope to plot an ''I-V'' curve. | |
| − | + | ||
| − | + | ||
| − | + | ''I-V'' curves usually show current on the vertical axis and voltage on the horizontal axis. Using the oscilloscope to plot ''V<sub>D1</sub>'' on the horizontal axis is easy. Just hook the channel 1 probe across the photodiode. | |
| − | + | It is not as straightforward to plot ''I<sub>diode</sub>''. The oscilloscope measures voltage, so first it is necessary to convert ''I<sub>D1</sub>'' to a voltage. This can be done by placing a resistor (R<sub>1</sub>) in series with the photodiode. The voltage across R<sub>1</sub> is proportional to the current through the photodiode. | |
| − | + | ||
| − | + | It's a little harder than you might anticipate to measure the voltage across R<sub>1</sub> with an oscilloscope. You might be tempted to hook the channel 2 probe across R<sub>1</sub>. Unfortunately, the ground leads of the oscilloscope probes are wired together. Connecting the probe in this way causes a short from R<sub>1</sub> to ground. Because the ground leads of the probes are wired together, it is a very good idea to hook probe ground clips only to the ground node of your circuit. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | An instrumentation amplifier produces an output equal to the difference between the voltages at its two input terminals. The instrumentation amplifier shown in the schematic diagram computes ''V<sub>R1</sub>'' = ''V<sub>in</sub>'' - ''V<sub>D1</sub>''. The input terminals of the instrumentation amplifier have very high input impedance, so current flowing into the instrumentation amplifier inputs is negligible. There are many kinds of instrumentation amplifiers available. In this lab, you will use an integrated circuit (IC) instrumentation amplifier, part number AD622 manufactured by Analog Devices. [[http://www.analog.com/static/imported-files/data_sheets/AD622.pdf Click here]] for the AD622 data sheet. | |
| − | + | ||
| − | + | [[Image:AD622Pinout.png|thumb|250px|right]] | |
| − | + | The instrumentation amplifier comes in an 8 pin plastic package called a dual-inline package (DIP). The leads on the package have the same spacing as the tie points on the breadboard, so the amplifier can be inserted directly into a breadboard. The arrangement of component leads for the instrumentation amplifier is shown at right. | |
| − | + | ||
| − | + | ||
| − | === | + | ====Construct the photodiode circuit==== |
| − | + | [[Image:PhotodiodeWith_AD622DiffAmp.png|300 px|thumb|Photodiode measurement circuit with AD622 instrumentation amplifier]] | |
| − | + | ||
| − | + | ||
| − | + | # Make sure your power supply is disabled. | |
| + | # Mount the instrumentation amplifier so that it straddles the notch. | ||
| + | # Connect the signals as shown in the schematic to pins 2 and 3. The output is pin 6. | ||
| + | #* Use a 10KΩ resistor for R1. | ||
| + | #* Connect the REF signal on the amplifier (pin 5) to ground. | ||
| + | # Configure the power supply for series mode. | ||
| + | # Set the power supply for +/- 15V. | ||
| + | #* In series mode, the negative terminal of the left supply will be at -15V. The positive terminal of the left supply and the negative terminal of the right supply will be connected together inside the power supply. This is the ground potential. The plus terminal of the right supply will be at +15V. | ||
| + | # Connect the power supply leads to the +V<sub>S</sub> and -V<sub>S</sub> pins: pins 7 and 4 will be at +15V and -15V, respectively. | ||
| − | === | + | ====Procedure==== |
| − | + | ||
| − | + | # Connect the function generator to provide ''V<sub>in</sub>'' to the circuit. Configure the function generator to apply a triangle wave between ± 1-3 V at 1 kHz. | |
| − | + | # Connect Channel 1 of the oscilloscope to ''V<sub>d</sub>''. | |
| − | + | # Connect Channel 2 of the oscilloscope to ''V<sub>R1</sub>'' (the output of the instrumentation amplifier). | |
| + | # Set the oscilloscope to X-Y display mode. | ||
| + | # With the photodiode covered, save the curve to a USB memory stick ([[Save_the_curve_to_a_USB_memory_stick|see abbreviated instructions]]). | ||
| + | # Load the curve into Matlab and plot the ''I-V'' curve | ||
| + | #* Remember to convert the resistor voltage to current. | ||
| + | # Repeat the measurement for several intensities of light illuminating the diode. | ||
| + | # '''Plot the curves for all light intensities on the same set of axes.''' | ||
| + | # '''What operating condition of the photodiode is best for measuring light intensity?''' | ||
| − | + | [[Image:Photodiode_Illuminated4x.gif|thumb|250px|center|Example photodiode ''I-V'' curves.]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <references /> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {{ | + | {{Template:20.309 bottom}} |
Latest revision as of 18:46, 7 April 2017
Overview
During the next lab exercise on measuring DNA melting curves, you will build and debug several electronic circuits. This bootcamp will introduce you to the electronic components and test equipment you will use. A short answer-book style writeup is required. Your writeup should include the practice problems and any bolded questions asked throughout the lab instructions. Don't forget the basics: report measurements with an appropriate number of significant figures, units, and uncertainty. Label plot axes.
This bootcamp requires an understanding of basic circuits. If you need to review circuit concepts, start with the Electronics Primer page. If you have a lot of experience with electronics, ask one of the instructors about doing a stimulating mini-project instead of the mini-lab assignment.
Problems
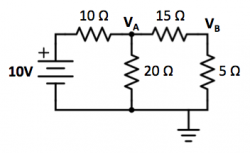
Question 1
Consider the following circuit composed of a network of resistors:
a) Combining resistance values in parallel and in series, draw a simplified version of the circuit containing the given voltage source (10V) and one equivalent resistor. Label the equivalent resistance value.
b) Find the voltage values for the nodes $ V_A $ and $ V_B $ in the above diagram.
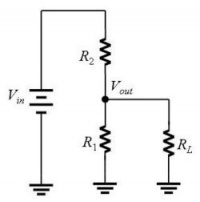
Question 2
Referring to the circuit shown below, what value of $ R_L $ (in terms of $ R_1 $ and $ R_2 $) will result in the maximum power being dissipated in the load?
Hint: this is much easier to do if you first remove the load, and calculate the equivalent Thevenin output resistance $ R_T $ of the divider looking into the node labeled $ V_{out} $. Then express $ R_L $ for maximal power transfer in terms of $ R_T $.
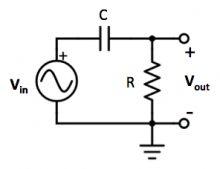
Question 3
In the following circuit, R = 10 kΩ and C = 10 nF.
a) Find the transfer function $ {V_{out} \over V_{in}} $.
b) What type of filter is this? Justify your answer.
c) What is the cutoff frequency of this filter? Write your answer in units of Hz. Remember that $ \omega = 2 \pi f $.
Note: You may find the pages on Impedance Analysis and Transfer Functions and Bode Plots helpful for this problem.
Lab Exercises
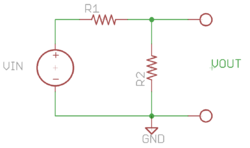
Voltage divider
In the first hands-on part of the bootcamp, you will analyze and build a voltage divider. The divider circuit comprises two resistors and a voltage source, as shown in the schematic diagram. You will select the values for R1 and R2.
Before you build
Choose any two resistor values you like, but there are a few practical constraints. The resistors in the lab range in value from 1 Ω to 10 MΩ. Within that range, manufacturers only produce certain standard values. Check the supply bins or this table to see which values are available.
Resistors convert electric power to heat. Since the ideal circuit model does not include heat energy, ideal resistors have the effect of making power disappear from a circuit. Of course, energy is conserved in a real circuit. The energy is converted to a form that is extrinsic to the ideal circuit model.
The fact that energy disappears from a circuit model doesn't mean that you can ignore it. Power dissipation in resistors increases in proportion to resistance and the square of current, $ P=I^2R $. Physical resistors must be able to shed their heat to the environment or else they tend to get very hot and fail. A noxious puff of smoke frequently accompanies failure. Even if a component operated at an excessive power level does not vaporize, it may no longer behave as specified. The maximum power rating of the resistors in the lab is ¼ Watt. Ensure that the power dissipated by R1 and R2 does not exceed the maximum rating for Vin values in the range of 0-15 V.
You will use an oscilloscope and a volt meter to measure voltages in the circuit. The oscilloscope has an input impedance of 1 MΩ. Connecting the oscilloscope probe to a node of the circuit is equivalent to placing a 1 MΩ resistor between that node and ground. In circuits that use very large resistors, the current flowing into the oscilloscope can significantly distort measurements.
Before building the divider circuit:
- Record the values you selected for R1 and R2.
- Find the gain of the circuit, $ ^{V_{out}}/_{V_{in}} $
- Plot an I-V curve with I on the vertical axis and Vin on the horizontal axis, over the range 0 V < Vin < 15 V.
- A hand-drawn plot is fine.
- What is the maximum power dissipated in each resistor between 0 V < Vin < 15 V?
Another practical issue: tolerance

It's easy enough to write down an exact value for a resistor like 15 kΩ or eπ Ω and analyze a circuit model that contains such a component. But fabricating a 15 kΩ or eπ Ω resistor is another matter. It is not possible to realize physical components with infinite precision. The values you specify on paper are called nominal values. Nominal means: "stated or expressed but not necessarily corresponding exactly to the real value."[1] When you go to build the circuit, the actual value of the resistors you use will be somewhat different than the nominal values you used to analyze the circuit.
To account for the difference between the nominal and actual values of a component, the manufacturer guarantees that the actual value will differ from the nominal value by no more than a certain amount. Resistor tolerances are usually specified as a percent of nominal value. Some common resistor tolerances are 10%, 5%, 2.5%, and 1%. Even smaller tolerances are available from some manufacturers — down to 0.05& in some cases. The resistors in the lab are guaranteed by the manufacturer to be within 5% of the nominal value.
Because the actual values of the resistors differ from the nominal values, the power dissipation in R1 and R2 will under some circumstances be greater than what you computed using the nominal values. To be safe, the best thing to do is compute the power dissipated in both resistors under worst-case assumptions.
Measure the resistors with a digital multimeter
Go ahead and get the resistors for your circuit from the bins in the lab.
The value of each resistor is indicated by a set of color-coded bands on the component body. Through negligence or malice of last semester's scholars, components occasionally end up in the wrong bin. Ensure that you have the correct resistors by reading the color bands. Instructions for reading resistor markings are available at this Wikipedia page.
Measure the actual value of both resistors with a digital multimeter (DMM). DMMs are multifunction instruments that usually include functions for measuring voltage, current, and resistance. They connect to component terminals through a pair of test leads. DMMs measure resistance by applying a small voltage across the test leads and measuring the resulting current flow. To get an accurate measurement of a resistor, its leads must be isolated from other circuit elements. If the resistor leads are connected to other components, current flowing through other paths will distort the measurement.
- Plug two test leads into the DMM.
- The black lead goes into the terminal labeled COM.
- The red lead plugs into different terminals depending on the measurement you are making. For resistance measurements, use the V Ω terminal. The A terminal is for current measurements.
- Select the resistance mode, which is labeled with an Ω symbol.
- If you've inserted your resistors on the breadboard, remove them and connect the DMM leads to the resistor that you want to measure.
- Measure your resistors and record their actual values.
From this point on, use the actual value instead of the nominal value in your calculations. Using the actual value will reduce the error in results that depend on R1 or R2.
Build the circuit
The next step is to build the divider circuit. If you have worked with electronic components before, you probably noticed that most of them look a little bit like bugs. They have a central body with some gangly legs sticking out, called leads. The leads carry current from the outside of a component to its innards where the magic happens. One of the first challenges facing an aspiring circuit maker is to properly connect all the bugs' legs whilst keeping the circuit robust and orderly. Solderless electronic breadboards are a convenient platform for building circuits that might require a lot of debugging or frequent reconfiguration. Breadboards are flexible and easy to use, but they have a few downsides. They have high interconnect capacitance and resistance. If you don't know why that's bad, pay closer attention in lecture.
Before you go on, gather the items that you will need:
- solderless electronic breadboard,
- lengths of different colored wire to make jump wires,
- wire strippers (located in the lab station tool drawers).
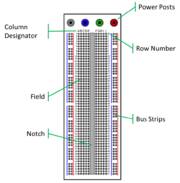
The image on the right shows an example of solderless electronic breadboard. The breadboard has a large number of square holes in it called tie points. A single wire or component lead fits into each tie point. Spring-loaded contacts inside each tie point hold leads in place and provide electrical connections.
Sets of tie points are electrically connected to each other in a pattern that allows just about any circuit arrangement to be realized on the breadboard. The two central grids of tie points separated by a notch are called the field. Each row of tie points in the field is called a terminal strip. Rows of terminal strips are numbered. Columns are designated by a letter. Within a terminal strip, the five tie points A-E are connected, and tie points F-J are connected. Points A-E are not connected to points F-J. Connections between component leads are made by running jump wires between tie points that are connected to each lead, as shown in the image above on the right.
The long lines of tie points to the left, right, and above the field are called bus strips. Bus strips are highlighted by red and blue lines. All of the tie points in a bus strip are connected together. Because most circuits have a lot of power and ground connections, the bus strips are almost always connected to the power supply. Using the bus strips as a power distribution network makes it easy to connect any terminal strip to power or ground with a short jump wire.
If you are unsure whether two holes on the breadboard are connected, insert short wires in the holes. Use the resistance or continuity features of the DMM to check if they are connected.
- Mount R1 on the breadboard by bending its leads at a 90 degree angle and trimming them to about half an inch long. Press the leads into the breadboard.
- Mount R2 so that one of its leads is in the same terminal strip as one of the leads from R1. This will create an electrical connection between the two resistors.
Connect the power supply
Now it's time to complete the circuit by connecting a voltage source. You will use a laboratory power supply to drive your circuit. The lab supply has three separate DC outputs called CH1, CH2, and CH3. Each supply has a + and - terminal, from which motivated electrons begin and end their journeys. [2] The CH1 and CH2 outputs are adjustable. The CH3 output always produces 5 volts with a current limit of 3 amps.
When you turn the power supply on, all three of the outputs will be disabled (which is a rather sensible way of doing things). Press the OUTPUT button to enable all three supplies. Press OUTPUT again to disable all three supplies.
Four dials on the front of the supply set the current and voltage limits for each of the two supplies from 0-20V and 0-3A. At all times, each adjustable supply will be either current or voltage limited. Multicolor LEDs indicate which limit is currently in effect: green for voltage-limited and red for current-limited. When the supply is disabled, the numeric displays will show the values of the limit settings. When the supply is in operation, the displays show the actual current and voltage values for each supply.
Two pushbuttons near the middle of the the lab supply control panel configure the interconnection of CH1 and CH2. There are 3 possible settings: independent, series, or parallel. In independent mode, CH1 and CH2 are not connected together. The two sets of voltage and current dials operate independently. In series mode, the plus terminal of CH2 supply is internally connected to the minus terminal of CH1. Both supplies operate with the same voltage limit. The current limits are independent. This provides a split supply with equal positive and negative voltages relative to the common terminal. In parallel mode, the + terminals of CH1 and CH2 are connected together, as are the - terminals. Parallel configuration allows a maximum possible current of 6 amps — 3 amps from each of the supplies.
The post labeled "GND" in green letters is connected to earth ground. Earth ground is a wire that runs through the third prong of the electrical plug to a post driven deep into the ground somewhere near Building 16. Earth ground is not needed for this lab.
In this part of the lab, you will use a 15 volt, split supply. Configure the lab supply in series mode with a voltage of 15 V and a current limit of about 0.1 amps on CH1 and CH2.
The breadboard has four colored post terminals at the top right to facilitate power supply connections. These are called banana post terminals. Each post terminal accepts a banana connector inserted at the top and a bare wire at the base. The banana terminals are not connected to any of the tie points, so it is necessary to run wires from the post terminals to tie points on the bus strips. Wires connected to the post should pass through the hole through the base of the post. Be sure that only bare wire touches the terminal. Insulation under the screw terminal may cause an intermittent connection. Secure the wire by tightening the colored plastic nut (onto bare wire, not insulation plastic sleeve).
Use jump wires to connect the power post terminals to the bus strips on the breadboard. Hook up the power as shown in the picture above (note that the circuit shown is not yet complete, however). Power the voltage divider circuit by connecting it to the +15 V bus strip and ground.
- Use the cutting jaws of the wire stripper to trim the resistor leads so that the component bodies will be close to the board.
- In addition to being untidy, leads that are too long may make unintentional contact with the metal under the breadboard.
- Don't cut the leads too short either, or they may not make good contact with the tie point.
- Mount the resistors by pressing their leads into tie points in the field.
- Run jump wires to connect the divider to the power and ground bus strips.
- Keep your wiring neat, close to the board, and easy to follow. A good way to do this is to route wires horizontally or vertically, making right-angle bends to change directions.
- Use the right length of wire. The right length of wire is the shortest length of wire that satisfies the previous guideline.
- Use the bus strips to distribute power supplies and ground as described in the text above.
Use a cable with banana connectors on both ends to connect the power supply to the posts. You can find banana cables hanging on the cable rake near the time travel poster. Refer back to left side of the lab map in lab orientation if you need to. Convention is to use black cables and connectors and blue bus strips for ground. Red bus strips are almost always used for power supplies.
The exposed metal screws on the bottom of the banana connectors (on the back side of the breadboard) can short to the metal optical table. Cover them with electrical tape to prevent a calamity.
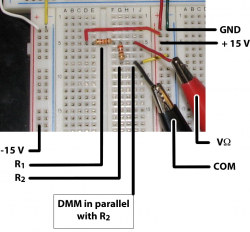
Measure voltage Vout
The DMM has modes for measuring DC and AC voltages. In DC mode, the meter reads the average value of the test signal. In AC mode, the meter reads the root-mean-square value of a time varying signal. In this lab you will use DC mode, which is labeled with a solid line above a dashed line.
- Switch the DMM to DC voltage mode and connect the DMM test leads. Insert the black lead into the receptacle marked COM and the red lead in VΩ.
- Connect the test leads across the terminals of R2.
- Record the voltage shown on the DMM for each input voltage Vin = 0, 2.5, 5, 10 and 15 V. Hint: You can make the +15 V bus strip whatever voltage you want simply by adjusting the voltage at the power supply.
The DMM has a very high input impedance. We can simulate the effect of an inferior meter with lower input impedance by adding a 1 kΩ resistor in parallel with R2.
- Add the 1 kΩ resistor in parallel with R2 and measure the voltage across R2. By what percentage did the measurement change?
- Remove the 1 kΩ resistor and the DMM from the circuit.
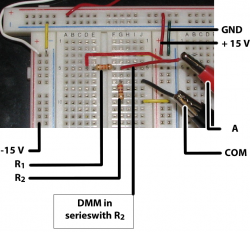
Measure current I
In order to measure current, you must move the red test lead from the VΩ receptacle on the DMM to the A receptacle. The reason for the change is that there is a fundamental difference between measuring voltage and current. Voltage is a measure of potential; current is a measure of flow. To make an accurate voltage measurement, the meter should have very high input impedance. High input impedance in a voltage measurement ensures that only a small percentage of the current flowing in the circuit goes through the meter. Measuring current essentially requires counting the number of electrons that flow past a certain point in a given time, so the opposite is true. To get a good count, all of the current must flow through the meter. Making a good current measurement requires a meter with very low input impedance. In addition, you must place the meter in series with the current you want to measure so that all of the current flows through the meter.
- Note: In the 20.309 lab, the Fluke 115 DMMs can accurately measure a few milliamps of current, while the 111 models should not be trusted at very low current levels. Click these links for full documentation for the (discontinued) Fluke 111 and Fluke 115 multimeters.
- For this section of the electronics mini-lab, feel free to swap R1 and R2 for smaller-value resistors, so the current flowing through R2 is large enough to be measured by your Fluke 11x ammeter. Simply make a note of the new resistor values and justify your choice in your lab report.
- Switch the DMM to DC current mode and configure the leads for current measurement.
- Move the red lead to the receptacle marked A.
- Positive current flows into the red lead and out of the black.
- Place the leads of the DMM in series with R2 as show in the image at right.
- Record the current through the circuit at each input voltage Vin = 0, 2.5, 5, 10 and 15 V
- Plot the measured I-V curve on the same set of axes as the calculated curve.
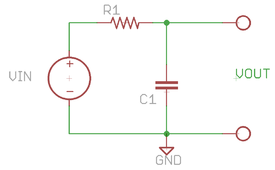
RC low-pass filter
In this part of the lab, you will replace R2 with a capacitor. This will transform your humdrum voltage divider circuit into a spectacular low-pass filter. You will measure the time constant and frequency response of the filter circuit. Capacitors are available in the lab with a range of values from 0.01 - 0.1 uF. Check the supply bins to see what is available and choose a value for C1.
- Choose a capacitor value and calculate the cutoff frequency of your filter.
- If the frequency is below 100 Hz or above 10 kHz, you might want to rethink your capacitor or resistor choice. Change either the resistor or capacitor to get a cutoff frequency in this range.
- Draw a Bode plot of the filter response using straight line segments to approximate the transfer function. (For help with drawing Bode plots, visit the page on Bode plots.)
- Replace R2 with a capacitor of the selected value.
Replace the power supply with a function generator
The behavior of ideal resistors is independent of frequency, so it was possible to measure the (frequency independent) transfer function of a voltage divider using the constant voltages produced by a lab power supply. Since the impedance of a capacitor varies in proportion to the inverse of signal frequency, it will be necessary to measure the response of the low-pass filter circuit over a range of frequencies. This requires a more sophisticated method of creating input voltages. Sine and square waves are especially useful for this task. In this part of the lab, you will also replace the power supply with a function generator, which is a piece of equipment that can generate several kinds of periodic signals: sine, triangle, and square waves. The amplitude and frequency of the function generator's output are adjustable.
There are several types of function generators in the lab. The digital function generators allow you to enter frequencies on a keypad. Press one of the unit keys (Hz, kHz or MHz) to complete your entry. Use the decade selector knob and frequency dial to set the frequency of the analog function generators. The output frequency is adjustable between about 0.01 Hz and 10 MHz. Amplitude ranges from 0.1 V to 10.0 V.
- Disable the power supply and disconnect it from the circuit.
- Connect a function generator in place of the power supply.
- Attach a BNC cable to the Output connector on the front right of the function generator.
- This circuit is sensitive to the parasitic capacitance added to a circuit by multiple jump-wire to tie-point connections, so use a BNC to grabby clip adapter to connect directly to the left side of the resistor as shown in the picture. Remove the jump wires between there and the +15 V bus strip.
- The connections can also be made using BNC to bare wire adapters found in the bins on the south wall.
- The center conductor of the BNC cable is the positive signal lead; the outer conductor/shield is the ground signal lead.
- Turn on the function generator.
- Set the frequency to 10 Hz.
- Select a sine wave output. (Press the WAVE button on the digital function generators or use the waveform knob on the analog generators.)
Connect an oscilloscope
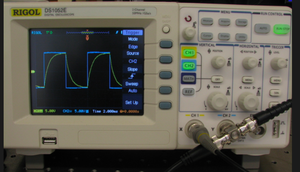
Oscilloscopes provide a graphic display of time-varying voltage signals. In the most frequently used mode, the oscilloscope screen shows a plot of voltage on the vertical axis versus time on the horizontal axis. The oscilloscopes in the lab have two inputs. Either or both of the inputs may be plotted. Two knobs adjust the voltage and time scales so that it is possible to display a wide range of waveforms. The display also includes status indicators and configurable waveform measurements such as amplitude, frequency, and phase.
Click these links for full documentation for the Rigol DS1052e and ATTEN ADS1022c oscilloscopes.
- Get two oscilloscope probes from the cable rakes on the wall next to the time machine poster.
- Connect the oscilloscope to the circuit. CH2 will monitor Vin, CH1 Vout.
- Connect the BNC connector of the first oscilloscope probe to the CH1 oscilloscope input. Connect the probe to Vout, the top of the capacitor, using a small jump wire held in the retractable clip at the end. Connect the black alligator clip to ground, the bottom of the capacitor. CH1 is thus in parallel with the capacitor.
- Using a BNC T-connector, attach the other oscilloscope probe to the CH2 input and to Vin from the function generator.
- Set the oscilloscope vertical scale for each channel to 5 V per division.
- The Rigol oscilloscopes have one knob that controls the vertical scale for both channels. Press one of the channel select buttons before you adjust the "vertical position" knob until the bottom-row display indicates "CH1 - 5.00V" and "CH2 - 5.00V".
- The ATTEN oscilloscopes have a knob for each channel. Software menu functions still require you to press the button for the desired channel.
- Make sure the scope triggers on CH2:
- The oscilloscope begins recording and displaying the waveform when it is triggered. There are several options to configure when the trigger occurs. One of the simplest modes causes a trigger when the input signal crosses a certain voltage level.
- On both the Rigol and the ATTEN oscilloscopes, press the "menu" button of the right "Trigger" panel, and on the screen select "CH2" as the "Source". Adjust the trigger level by rotating the "Level" knob.
Measure and plot the transfer function
- Set up the signal generator for 5 V peak-to-peak, sine wave output.
- Select sine-wave mode using the mode buttons.
- Set the peak-to-peak amplitude of the signal generator's output to 5 V using the "Ampl" tab on the function generator.
- Use the "Freq" tab on the signal generator to select a frequency of 10 Hz.
- Adjust the horizontal scale on the oscilloscope to display about 3 periods of the sine wave.
- Record the peak-to-peak amplitude of Vout</sum> and Vin.
- The oscilloscope has a built-in feature for measuring peak-to-peak voltages that will make your life much easier.
- Press the "Measure" button in the "Menu" top panel
- Choose the channel of interest under "Source"
- Choose "Vp-p".
- The oscilloscope has a built-in feature for measuring peak-to-peak voltages that will make your life much easier.
- Repeat the measurement of Vout and Vin at frequencies of 100 Hz, 1 KHz, 10 KHz, 100 KHz, 1 MHz, and several frequencies in the vicinity of the cutoff frequency.
- Make a Bode plot
- Plot the measured values of $ \frac{V_{out}}{V_{in}} $ versus frequency on the same set of axes as your Bode plot.
Identify unknown filter circuits
In this part of the lab, you will measure the transfer function of four filter circuits made out of resistors and capacitors. The circuits will be hidden inside blue boxes marked A through D. Your goal is to figure out what type of circuit is inside of each "black box."
All of the boxes have two BNC connectors. You will use a function generator to drive sine waves of various frequencies into one connector and an oscilloscope to measure the resulting output on the other connector. Input and output are marked on the box.
Measure each box at each decade of frequency between 10 Hz and 1 MHz. You may want to measure choose additional frequencies in transition regions. The transfer function consists of two plots: one that shows the magnitude of the output divided by the magnitude of the input as a function of frequency; and another that shows the phase difference between the input and the output. The former is the Bode gain plot like that for your RC filter. The latter is the Bode phase plot. From those plots, you can derive the topology of the circuits inside and determine the cutoff frequencies of each filter.
- Use BNC cables to connect the function generator and oscilloscope to a box.
- Set the scope to trigger from the input channel.
- Measure the input, output, and phase difference at a range of frequencies.
- Make sure to take enough measurements to completely identify the transfer function.
- Take extra measurements in the vicinity of the cutoff frequency or frequencies.
- Generate the Bode gain plot and the Bode phase plot for each of the four black (blue) boxes: A through D.
- Draw the circuit inside each box.
- Optional: In Matlab, use nlinfit to fit parameters of a transfer function for each circuit.
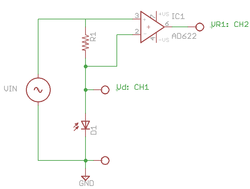
Photodiode I-V curve
In this part of the lab, you will examine how light falling on a photodiode affects its I-V characteristic. You will use a function generator and an instrumentation amplifier to make simultaneous measurements of voltage across and current through the photodiode and plot an I-V curve on an oscilloscope.
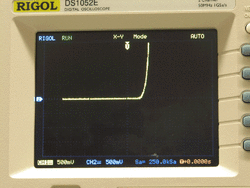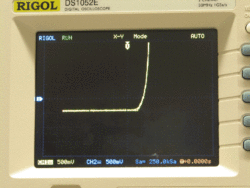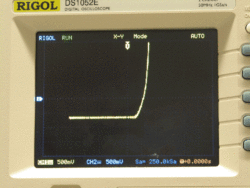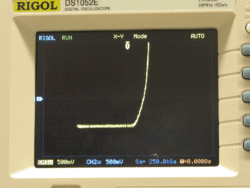
In the preceding sections of this lab, you used an oscilloscope to plot voltage signals versus time. The oscilloscope also has an X-Y mode. In X-Y mode, the oscilloscope plots channel 1 on the horizontal axis versus channel 2 on the vertical axis. Using X-Y mode, it is possible to use an oscilloscope to plot an I-V curve.
I-V curves usually show current on the vertical axis and voltage on the horizontal axis. Using the oscilloscope to plot VD1 on the horizontal axis is easy. Just hook the channel 1 probe across the photodiode.
It is not as straightforward to plot Idiode. The oscilloscope measures voltage, so first it is necessary to convert ID1 to a voltage. This can be done by placing a resistor (R1) in series with the photodiode. The voltage across R1 is proportional to the current through the photodiode.
It's a little harder than you might anticipate to measure the voltage across R1 with an oscilloscope. You might be tempted to hook the channel 2 probe across R1. Unfortunately, the ground leads of the oscilloscope probes are wired together. Connecting the probe in this way causes a short from R1 to ground. Because the ground leads of the probes are wired together, it is a very good idea to hook probe ground clips only to the ground node of your circuit.
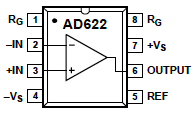
An instrumentation amplifier produces an output equal to the difference between the voltages at its two input terminals. The instrumentation amplifier shown in the schematic diagram computes VR1 = Vin - VD1. The input terminals of the instrumentation amplifier have very high input impedance, so current flowing into the instrumentation amplifier inputs is negligible. There are many kinds of instrumentation amplifiers available. In this lab, you will use an integrated circuit (IC) instrumentation amplifier, part number AD622 manufactured by Analog Devices. [Click here] for the AD622 data sheet.
The instrumentation amplifier comes in an 8 pin plastic package called a dual-inline package (DIP). The leads on the package have the same spacing as the tie points on the breadboard, so the amplifier can be inserted directly into a breadboard. The arrangement of component leads for the instrumentation amplifier is shown at right.
Construct the photodiode circuit
- Make sure your power supply is disabled.
- Mount the instrumentation amplifier so that it straddles the notch.
- Connect the signals as shown in the schematic to pins 2 and 3. The output is pin 6.
- Use a 10KΩ resistor for R1.
- Connect the REF signal on the amplifier (pin 5) to ground.
- Configure the power supply for series mode.
- Set the power supply for +/- 15V.
- In series mode, the negative terminal of the left supply will be at -15V. The positive terminal of the left supply and the negative terminal of the right supply will be connected together inside the power supply. This is the ground potential. The plus terminal of the right supply will be at +15V.
- Connect the power supply leads to the +VS and -VS pins: pins 7 and 4 will be at +15V and -15V, respectively.
Procedure
- Connect the function generator to provide Vin to the circuit. Configure the function generator to apply a triangle wave between ± 1-3 V at 1 kHz.
- Connect Channel 1 of the oscilloscope to Vd.
- Connect Channel 2 of the oscilloscope to VR1 (the output of the instrumentation amplifier).
- Set the oscilloscope to X-Y display mode.
- With the photodiode covered, save the curve to a USB memory stick (see abbreviated instructions).
- Load the curve into Matlab and plot the I-V curve
- Remember to convert the resistor voltage to current.
- Repeat the measurement for several intensities of light illuminating the diode.
- Plot the curves for all light intensities on the same set of axes.
- What operating condition of the photodiode is best for measuring light intensity?
- ↑ http://www.merriam-webster.com/dictionary/nominal
- ↑ Don't read this if you think you understand circuits. The electrons begin their journey at the minus terminal; however, positive current is defined to flow from plus to minus. It's all <a href="http://www.allaboutcircuits.com/vol_1/chpt_1/7.html">Benjamin Franklin's fault</a>.
</div>