Review of probability concepts

Probability review

This quick review of probability concepts is a work in progress.

Random distributions

Plots of PDF $ f_x(x) $ vs. $ x $ and CDF $ F_x(x) $ vs $ x $ for the uniform distribution on the interval (0,1) and the normal distribution with $ \mu=0 $ and $ \sigma=1 $. MATLAB functions rand and randn return pseudorandom values that follow these distributions.

The question of what exactly a random variable is can get a bit philosophical. For present purposes, let's just say that a random variable represents the outcome of some stochastic process, and that you have no way to predict what the value of variable will be.

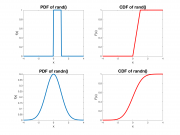
Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a Probability Density Function (PDF), usually written as $ f_x(x) $. Two commonly-used PDFs are shown in the plots on the right. Larger values of the PDF indicate more likely outcomes.

The probability that a continuous random variable will take on a particular value such as 0.5 is (perhaps counter-intuitively) zero. This is because there are an infinite number of possible outcomes. The chance of getting exactly 0.5 when there are an infinite set of possible outcomes is equal to one divided by infinity. In other words, there is no chance at all of getting exactly 0.5. This is kind of baffling to think about and certainly annoying to work with. It's frequently cleaner to work with intervals. The chance that a random variable will fall between two numbers $ a $ and $ b $ can be found by integrating the PDF from $ a $ to $ b $:

$ Pr(a \leq x \leq b)=\int_a^b f(x) $

The Cumulative Distribution Function $ F_x(x) $ is equal to the integral of the PDF from $ -\infty $ to $ x $:

$ F_x(x)=\int_{-\infty}^x f_x(\tau) d\tau $

$ F_x(x) $ is the probability that $ x $ takes on a value less than $ x $. Using the CDF, it easy to calculate probability that $ x $ falls within the interval $ [a,b] $:

$ Pr(a \leq x \leq b)=F_X(b)-F_x(a) $.

Mean, variance, and standard deviation

If you average a large number of outcomes of a random variable $ x $, the result approaches the variable's mean value $ \mu_x $:

$ \lim_{N\to\infty} \frac{1}{N} \sum_{1}^{N}{x_n}=\mu_x $

The mean can also be found from the PDF by integrating every possible outcome multiplied by its likelihood:

$ \mu_x=E(x)=\int_{−\infty}^{\infty}{x P(x) dx} $.

Standard deviation $ \sigma_x $ quantifies how far a random variable is likely to fall from its mean. Variance $ \sigma_x^2 $ is equal to the standard deviation squared. Sometimes, it is easier to work with variance in calculations. Most often, the interpretation of standard deviation is more intuitive than variance.

$ \sigma_x^2=\lim_{N\to\infty} \frac{1}{N} \sum_{1}^{N}{(x_n-\mu_x)^2} $

Variance can also be calculated from the PDF:

$ \sigma^2_x=\int_{−\infty}^{\infty}{(x-\mu)^2 P(x)dx} $

Calculations with random variables

If you add two random variables, their means add. Their variances also add. Standard deviations add under a big 'ol square root.

$ \mu_{x+y}=\mu_x+\mu_y $

$ \sigma_{x+y}^2=\sigma_x^2+\sigma_y^2 $

$ \sigma_{x+y}=\sqrt{\sigma_x^2+\sigma_y^2} $

Averaging

If you average N independent outcomes of a random variable, the standard deviation of the average is equal to

$ \sigma_{\bar{x},N}=\frac{\sigma_x}{\sqrt{N}} $

The standard deviation decreases in proportion to the square root of the number of averages. The term independent means that each outcome does not depend in any way on any other outcome.

Useful distributions

Binomial distribution

The binomial distribution considers the case where the outcome of a random variable is the sum of many individual go/no-go trials. The distribution assumes that the trials are independent and that the probability of success, $ p $, for each trial is the same. An example of a process that is well-modeled by the binomial distribution is the number of heads in 100 coin tosses. On each toss, the probability of success (heads) is $ p=0.5 $. If $ N $ is the number of trials, the average number of successes is equal to $ Np $. If you toss the coin 100 times, you expect on average to get 50 heads. The binomial distribution answers the question: "How surprised should I be if I get 12 heads?" The probability mass function (PMF) for a random variable x ~ B(N, p) gives the probability of getting exactly k successes in N trials:

$ Pr(k;n,p) = \Pr(x = k) = {n\choose k}p^k(1-p)^{n-k} $

for k = 0, 1, 2, ..., n, where

$ \binom n k =\frac{n!}{k!(n-k)!} $

(This is called a PMF instead of a PDF because it is discrete — the only possible outcomes are integers between 0 and N.)

The standard deviation of a binomial distribution is:

$ \sigma_x^2=np(1-p) $

Poisson distribution

Sometimes, it is useful to model a binary process where you know the average value of the process, but not N and p. If p is small ($ p<<1 $), it is straightforward to make the approximation $ (1-p)=1 $. When p is small, a very good approximation of the variance is:

$ \sigma_x^2=np $

The variance of a Poisson-distributed variable is equal to its mean. The Poisson distribution is a useful model for photon emission, radioactive decay, the number of letters you receive in the mail, the number of page requests on a certain website, the number of people who get in line to check out at a store, and many other everyday situations. The ability to estimate the variability of a binary process without knowing N and p is incredibly useful.

Normal distribution. Each band has a width of 1 standard deviation

Normal distribution

The normal distribution (also frequently called a Gaussian distribution or a bell curve is specified by two parameters, an average value $ \mu $, and a standard deviation $ \sigma $:

$ f(x \; | \; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2} } \; e^{ -\frac{(x-\mu)^2}{2\sigma^2} } $

In the normal distribution, about 68% of outcomes fall within the interval $ \mu \pm \sigma $, about 95% in the interval $ \mu \pm 2 \sigma $, and about 99.7% in the interval $ \mu \pm 3 \sigma $

Central Limit Theorem

If you add together a bunch of independent random variables, their sum tends to look like a normal distribution.