Estimating second order system parameters from noise power spectra using nonlinear regression

… the safe use of regression requires a good deal of thought and a good dose of skepticism

—Arnold Barnett

If your program generates an error message rather than curve fitting results, you probably won’t be able to make sense of the exact wording of the message.

—Motulsky and Shristopoulos. Fitting Models to Biological Data using Linear and Nonlinear Regression

Overview

In the limits of detection lab, you will use regression to estimate the parameters of second order system models of the optical trap and atomic force microscope (AFM). MATLAB includes a powerful nonlinear regression function called nlinfit. Like all sharp tools, nlinfit must be used with care. Nonlinear regression is like a chainsaw. In skilled hands, it is a powerful tool that produces breathtaking and sublime results. Inattentive or unskilled operation, on the other hand, usually engenders distorted, ugly, or even catastrophic outcomes.

Many common regression mistakes spawn subtle errors rather than total disasters. Because of this, bad regressions easily masquerade as good ones — hiding their insidious flaws behind a lovely, plausible pair of overlapping curves. In the spirit of of the gruesome accident videos your high-school gym teacher made you watch in drivers' ed., this page illustrates several tragic regressions and offers some hints for safely and accurately fitting power spectra obtained from the AFM and optical trap.

Remain vigilant at all times when you regress.

Regression concepts review

Nonlinear regression is a method for finding the relationship between a dependent variable $ y_n $ and an independent variable $ x_n $. The two quantities are related by a model function $ f(\beta, x_n) $. $ \beta $ is a vector of model parameters. The dependent variable $ y_n $ is measured in the presence of random noise, which is represented mathematically by a random variable $ \epsilon_n $. In equation form:

$ y_n=f(\beta, x_n)+\epsilon_n $.

The goal of regression is to find the set of model parameters $ \hat{\beta} $ that best matches the observed data. Because the dependent variable includes noise, the best fit parameter values $ \hat{\beta} $ will differ from the true values $ \beta $.

Ordinary nonlinear least squares regression assumes that:

• the independent variable is known exactly, with zero noise,
• the error values are independent and are all values of $ \epsilon_n $ are drawn from the same distribution (i.i.d),
• the distribution of the error terms has a mean value of zero,
• the independent variable covers a range adequate to define all the model parameters, and
• the model function exactly relates $ x $ and $ y $.

These assumptions are almost never perfectly met in practice. It is important to consider how badly the regression assumptions have been violated when assessing results.

Get ready …

You need four things to run a regression:

1. a vector containing the values of the independent variable;
2. a vector containing the corresponding observed values of the dependent variable;
3. a model function; and
4. a vector of initial guesses for the model parameters.

Power spectrum of x-axis QPD voltage. 3.2 μm silica spheres trapped with 80 mW laser power. Sampling frequency was 50 MHz.

Independent variable and observations

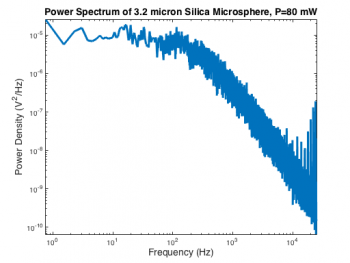
The second order system model of the optical trap makes predictions about the power spectrum of a thermally excited, trapped microsphere, whereas the instrument actually records a time sequence of voltages from the QPD position detector. The raw data must be converted into a power spectrum before fitting.

MATLAB has a function called pwelch that computes a power spectrum $ P_{xx}(f) $ and associated frequency bin vector $ f $ from a time series. Like many MATLAB functions, there are several different ways to invoke pwelch. Even judging by Mathworks' low standards for clarity and consistency, the various forms of pwelch are perplexing. Here is the command that generated the spectrum on the right:

[ Pxx, frequency ] = pwelch( OpticalTrapTimeDataX, [], [], [], 50000 );

The first argument, OpticalTrapTimeDataX is an Nx1 vector containing the QPD x-axis voltage samples. Empty values for the next three parameters (window, noverlap, and f) leave them set to their default values. The last argument is the sampling frequency, $ f_s $. We will reexamine the default parameter settings later on.

In order to make the best choice of independent and dependent variables, it is necessary to consider the relative influence of measurement noise on the two quantities in the regression: frequency and power density. The optical trap has a very accurate and precise oscillator circuit that generates its sample clock. This high-quality timebase allows frequencies in the QPD signal to be determined with almost no error. Power density, on the other hand, is inherently noisy due to constant perturbation of the trapped particle's position by the random thermal driving force. You can see how wiggly the power spectrum is in the vertical direction.

It's an easy choice: frequency will serve as the independent variable in the regression and power density will be the dependent variable.

Model function

nlinfit requires that the regression model be expressed as a function that takes two arguments and returns a single vector of predicted values. The signature of the model function must must have the form:

[ PredictedValues ] = ModelFunction( Beta, X ).

The first argument is a vector of model parameters. The second argument is a vector of independent variable values. The return value must must have the same size as the second argument.

The MATLAB function below models the power spectrum of a second-order system excited by white noise. The three model parameters are passed to the function in a 1x3 vector: undamped natural frequency $ f_0 $, damping ratio $ \zeta $, and low-frequency power density $ P_0 $.

function [ PowerDensity ] = SecondOrderSystemPowerSpectrum( ModelParameters, Frequency )
    
    undampedNaturalFrequency = 2 * pi * ModelParameters(1);
    dampingRatio = ModelParameters(2);
    lowFrequencyPowerDensity = ModelParameters(3);

    s = 2i * pi * Frequency;

    response = lowFrequencyPowerDensity * undampedNaturalFrequency.^2 ./ ...
        ( s.^2 + 2 * undampedNaturalFrequency * dampingRatio * s + undampedNaturalFrequency.^2 );
    
    PowerDensity = abs( response ).^2;

end

Initial guesses

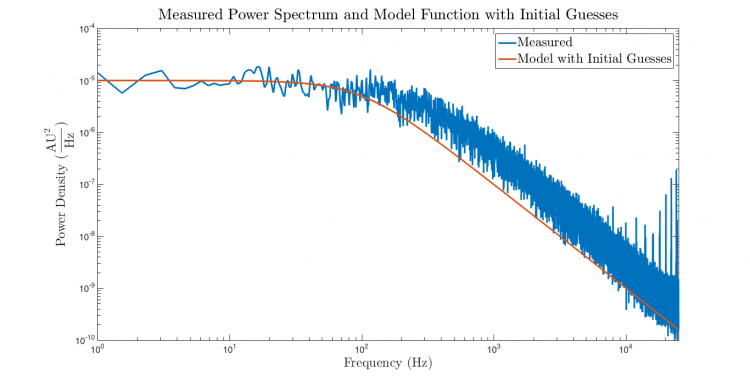
nlinfit infers the dimensionality of the regression (i.e. the number of model parameters) from the size of the Initial guess vector. Accordingly, the initial guesses should be stored in a 1x3 vector. A reasonable place to start is: 500 Hz for $ f_0 $, the average power density of the first 20 frequency bins for $ P_0 $, and 1 for the damping ratio.

Get set …

The first step of all regressions is to plot the data and the model function evaluated with the initial guesses on the same set of axes. The importance of this step cannot be overstated. You have almost no hope of succeeding if you skip this step. Symptoms of premature regression include confusion, waste of time, fatigue, irritability, alopecia, and feelings of frustration. Debugging regression problems is tricky. Do this plot to catch problems with the arguments to nlinfit early on. If the plot doesn't look right, fix the problem before proceeding. There is no chance that nlinfit will succeed if there is a problem with one of its arguments.

Go ahead ... do the plot.

Go ... first attempt

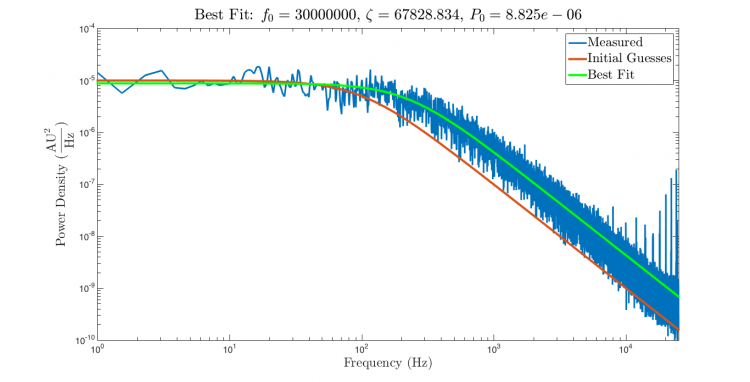
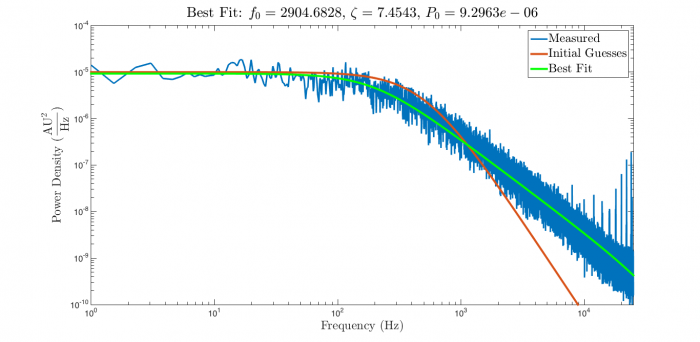
Here are the results of running nlinfit with the data, model, and initial guesses developed so far:

Success! Great curves!

Unfortunately, there was one troubling sign that something may have gone wrong. MATLAB barfed up a long and impenetrable word salad of foreboding verbiage on the console output:

Warning: Some columns of the Jacobian are effectively zero at the solution, indicating that 
the model is insensitive to some of its parameters.  That may be because those parameters 
are not present in the model, or otherwise do not affect the predicted values.  It may also be 
due to numerical underflow in the model function, which can sometimes be avoided by choosing 
better initial parameter values, or by rescaling or recentering.  Parameter estimates may be 
unreliable. 
> In nlinfit (line 373)

William Shatner in Nick of Time.

This unavailing communiqué is so perfectly unclear that it's impossible to know what the proper reaction is. Deep concern? Annoyance? Fear? Rage? Apathy? (It's just a warning, after all.) We will come back to the warning later. For now, you will have to take it on faith that red text coming from nlinfit is never good news, but it is not always bad news. (This particular warning offers some downright bad advice and no clue at all to the real, underlying problem.)

When it comes to error messages and warnings, nlinfit works just like the Mystic Seer that featured prominently in the unforgettable 43rd Twilight Zone episode Nick of Time starring William Shatner as a superstitious newlywed with car trouble and Patricia Breslin as his sensible bride.

Get out of town while you can.

Assessing the regression 1: examine the residuals

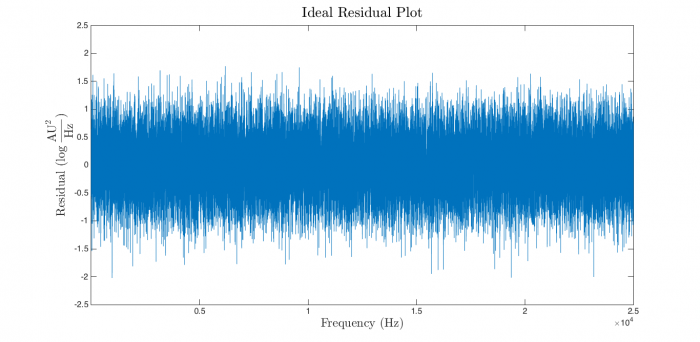
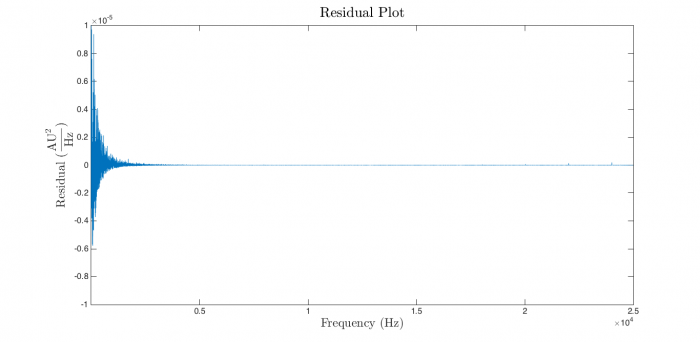
Violations of the regression assumptions are a leading cause of trouble. After every regression, do the responsible thing: spend a little time ascertaining how disgraceful the sin you just committed was. A good first step is to plot the residuals and have a look at them. (The second value returned from nlinfit contains a vector of the residuals.) If the regression assumptions are perfectly met, the plot should look something like this:

It's easy to convince yourself that the residuals in the plot above are independent and identically distributed. Compare that to the residual plot for the current regression:

This is terrible news. The residual plot doesn't bear even cursory examination. It is obvious that the magnitude of the residuals decreases dramatically as frequency increases — a significant and unacceptable violation of the regression assumptions. We definitely have a bad regression on our hands.

Attempt #2

The issue with the first regression is that the assumed distribution of the error terms was not a good model for what actually happened. In retrospect, this problem should have been obvious from a quick glance at the power spectral density plot. The magnitude of the noise (fuzz on the line) appears to be constant on a log scale — which means that it is not constant at all on a linear scale. Recalling that $ \log{ab}=\log{a}+log{b} $, it is clear that multiplicative error is a much better model of the uncertainty in the noise power spectrum than additive noise:

$ y_n=f(\beta,x_n)\epsilon_n $

This type of error is an inherent feature of the noise power spectrum. The uncertainty in each power density value is not constant. It is proportional to the value.

Fortunately, there are a few easy ways to fix this problem. One approach is to transform the dataset into log space:

$ \log{y_n}=\log{f(\beta,x_n)\epsilon_n}=\log{f(\beta,x_n)}+log{\epsilon_n} $

Taking the log of the dependent variable turns multiplicative noise into additive noise. ($ \epsilon_n $ is assumed to have an approximately log-normal distribution.) The code below uses MATLAB's anonymous function syntax to create a log-space model function.

logModelFunction = @( p, f ) log( SecondOrderSystemPowerSpectrum( p, f ) );

Simple enough. Now call nlinfit with logModelFunction instead of @ModelFunction. Remember to also take the log of $ P_{xx} $.

Here are the results:

Note that the estimate of $ f_0 $ changed by more than 250 Hz.

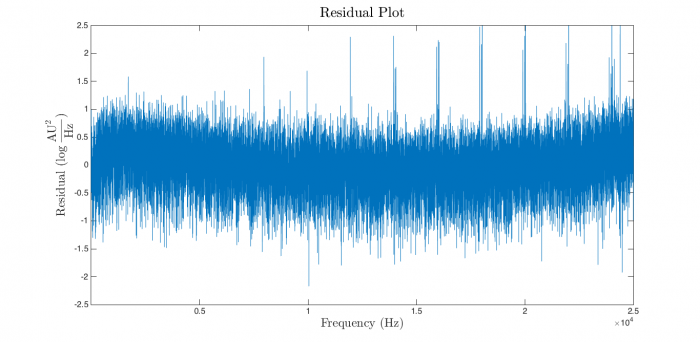
And the residual plot:

The residua plot much better. There is some systematic error evident, but the distribution looks a great deal more like the ideal plot.

MATLAB's warning this time is much shorter (but not more helpful):

Warning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be
estimated well (they are not identifiable).  Use caution in making predictions. 
> In nlinfit (line 376) 

In general, the less red text that nlinfit the better.

Assessing the regression take 2: parameter confidence intervals

Range of independent variable

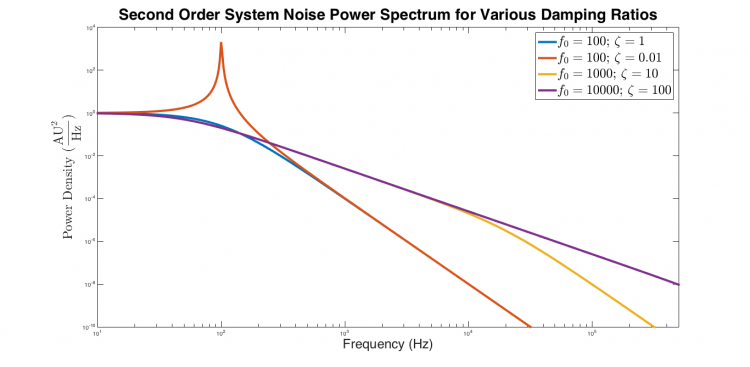
Power spectra of critically damped, underdamped, and overdamped second order systems excited by white noise. The underdamped response is flat at low frequencies, exhibits a narrow peak near $ f_0 $, and decreases with slope -4 at high frequencies. The critically damped response is flat from low frequency until approximately $ f_0 $, after which it falls with a slope of -4. Both overdamped systems are flat at low frequencies. They decrease with slope -2 at intermediate frequencies from approximately $ \frac{f_0}{\zeta} $ to $ f_0 $, after which the response decreases with slope -4.

Comparing the three regressions