Estimating second order system parameters from noise power spectra using nonlinear regression

… the safe use of regression requires a good deal of thought and a good dose of skepticism

—Arnold Barnett

Overview

In the limits of detection lab, you will use regression to estimate the parameters of second order system models of the optical trap and atomic force microscope (AFM). MATLAB includes a powerful nonlinear regression function called nlinfit. Like all sharp tools, nlinfit must be used with extreme care. Nonlinear regression is like a chainsaw. In the right hands, it is a powerful tool that produces breathtaking and sublime results. Inattentive or unskilled operation, on the other hand, usually engenders distorted, ugly, or even catastrophic outcomes.

Many common regression missteps spawn subtle errors instead of disasters. Because of this, bad regressions easily masquerade as good ones — hiding their insidious flaws behind a lovely, plausible pair of overlapping curves. This page illustrates several flawed regressions with the hope of helping you navigate the concealed hazards of fitting power spectra.

Remain vigilant at all times when you regress.

Regression review

Nonlinear regression is a method for finding the relationship between a dependent variable $ y_n $ and an independent variable $ x_n $. The two quantities are related by a model function $ f(\beta, x_n) $. $ \beta $ is a vector of model parameters. $ y_n $ is measured in the presence of random noise, which is represented mathematically by a random variable $ \epsilon_n $. In equation form:

$ y_n=f(\beta, x_n)+\epsilon_n $.

The goal of regression is to find the set of model parameters $ \hat{\beta} $ that best matches the observed data.

Ordinary nonlinear least squares regression assumes that:

• the independent variable is known exactly, with zero noise,
• the distribution of the error terms are independent and all drawn from the same distribution (i.i.d),
• the distribution of the error terms has a mean value of zero,
• the independent variable covers a range adequate to define all the model parameters, and
• the model function exactly relates $ x $ and $ y $.

These assumptions are almost never perfectly met in practice. It is important to consider how badly these assumptions have been violated when assessing regression results.

Get ready …

You need four things to run a regression:

1. a vector containing the values of the independent variable;
2. a vector containing the corresponding observed values of the dependent variable;
3. a model function; and
4. a vector of initial guesses for the model parameters.

Power spectrum of x-axis QPD voltage. 3.2 μm silica spheres trapped with 80 mW laser power. Sampling frequency was 50 MHz.

Independent variable and observations

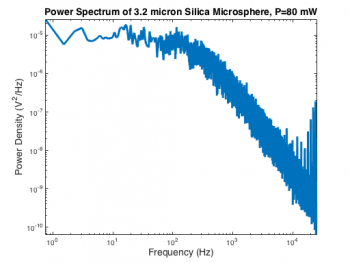
The second order system model of the optical trap makes predictions about the power spectrum of a thermally excited, trapped microsphere, whereas the instrument actually records a time sequence of voltages from the QPD position detector. The raw data must be converted into a power spectrum before fitting.

MATLAB has a function called pwelch that computes a power spectrum $ P_{xx}(f) $ and associated frequency bin vector $ f $ from a time series. Like many MATLAB functions, there are several different ways to invoke pwelch. Even judging by Mathworks' low standards for clarity and consistency, the various forms of pwelch are perplexing. Here is the command that generated the spectrum on the right:

[ Pxx, frequency ] = pwelch( OpticalTrapTimeDataX, [], [], [], 50000 );

The first argument, OpticalTrapTimeDataX is an Nx1 vector containing the QPD x-axis voltage samples. Empty values for the next three parameters (window, noverlap, and f) leave them set to their default values. The last argument is the sampling frequency, $ f_s $. We will reexamine the default parameter settings later on.

In order to make the best choice of independent and dependent variables, it is necessary to consider the relative influence of measurement noise on the two quantities in the regression: frequency and power density. The optical trap has a very accurate and precise oscillator circuit that generates its sample clock. This allows frequencies to be computed with tiny error. Power density, on the other hand, is inherently noisy due to constant perturbation of the trapped particle's position by the random thermal driving force. You can see how wiggly the power spectrum is in the vertical direction. It's an easy choice: frequency will serve as the independent variable in the regression and power density will be the dependent variable.

Model function

nlinfit requires that the regression model be expressed as a function that takes two arguments and returns a single vector of predicted values. The signature of the model function must must have the form:

[ PredictedValues ] = ModelFunction( Beta, X ).

The first argument is a vector of model parameters. The second argument is a vector of independent variable values. The return value must must have the same size as the second argument.

The MATLAB function below models the power spectrum of a second-order system excited by white noise. The three model parameters are passed to the function in a 1x3 vector: undamped natural frequency $ f_0 $, damping ratio $ \zeta $, and low-frequency power density $ P_0 $.

function [ PowerDensity ] = SecondOrderSystemPowerSpectrum( ModelParameters, Frequency )
    
    undampedNaturalFrequency = 2 * pi * ModelParameters(1);
    dampingRatio = ModelParameters(2);
    lowFrequencyPowerDensity = ModelParameters(3);

    s = 2i * pi * Frequency;

    response = lowFrequencyPowerDensity * undampedNaturalFrequency.^2 ./ ...
        ( s.^2 + 2 * undampedNaturalFrequency * dampingRatio * s + undampedNaturalFrequency.^2 );
    
    PowerDensity = abs( response ).^2;

end

Initial guesses

nlinfit infers the dimensionality of the regression (i.e. the number of model parameters) from the size of the Initial guess vector. Accordingly, the initial guesses should be stored in a 1x3 vector. A reasonable place to start is: 500 Hz for $ f_0 $, the average power density of the first 20 frequency bins for $ P_0 $, and 1 for the damping ratio.

Get set …

Observed data and model function with initial guesses.

The first step of all regressions is to plot the data and model function evaluated with the initial guesses on the same set of axes. The importance of this step cannot be overstated. Consequences of skipping this step can be tragic. Symptoms of premature regression initiation include confusion, waste of time, fatigue, irritability, alopecia, and feelings of frustration. Debugging regression problems is tricky. Take the time to do this plot in order to catch problems early. If the plot doesn't look right, there is no chance that nlinfit will succeed.

Go ahead ... do the plot.

Go ... first attempt

Range of independent variable

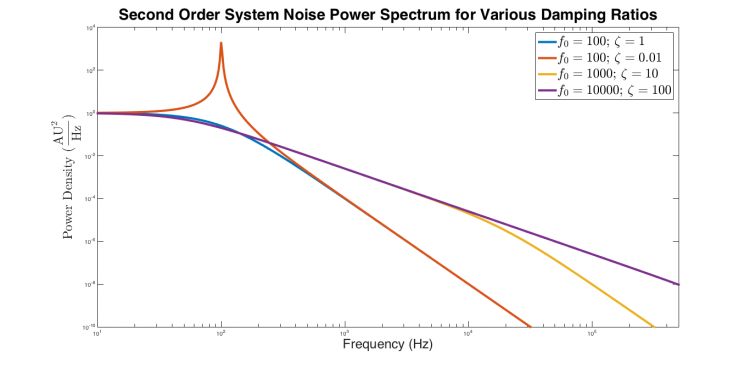
Power spectra of critically damped, underdamped, and overdamped second order systems excited by white noise. The underdamped response is flat at low frequencies, exhibits a narrow peak near $ f_0 $, and decreases with slope -4 at high frequencies. The critically damped response is flat from low frequency until approximately $ f_0 $, after which it falls with a slope of -4. Both overdamped systems are flat at low frequencies. They decrease with slope -2 at intermediate frequencies from approximately $ \frac{f_0}{\zeta} $ to $ f_0 $, after which the response decreases with slope -4.