Estimating second order system parameters from noise power spectra using nonlinear regression

… the safe use of regression requires a good deal of thought and a good dose of skepticism

Overview

In the limits of detection lab, you will use regression to estimate the parameters of second order system models of the optical trap and AFM. MATLAB includes a powerful nonlinear regression function called nlinfit. Like all sharp tools, nlinfit must be used with extreme care. Regression is a delicate business.

Many common regression missteps spawn subtle errors rather than catastrophic failures. Because of this, bad regressions easily masquerade as good ones — hiding their insidious flaws behind a lovely, plausible pair of overlapping curves. This page illustrates several flawed regressions with the hope of helping you navigate the concealed hazards of fitting power spectra.

Remain vigilant at all times when you regress.

Regression review

Nonlinear regression is a method for finding the relationship between a dependent variable $ y_n $ and an independent variable $ x_n $. The two quantities are related by a model function $ f(\beta, x_n) $. $ \beta $ is a vector of model parameters. $ y_n $ is measured in the presence of random noise, which is represented mathematically by a random variable $ \epsilon_n $. In equation form:

$ y_n=f(\beta, x_n)+\epsilon_n $.

The goal of regression is to find the set of model parameters $ \hat{\beta} $ that best matches the observed data.

Ordinary nonlinear least squares regression assumes that:

• the error terms have a mean value of zero,
• the error terms are independent and identically distributed (i.i.d.),
• the independent variable is known exactly, with zero noise, and
• the independent variable covers a range adequate to define all the model parameters.

These assumptions are almost never perfectly met in practice. It is important to consider how badly these assumptions have been violated when evaluating the results of a regression.

Get ready …

You need four things to run a regression:

1. a vector containing the values of the independent variable;
2. a vector containing the corresponding observed values of the dependent variable;
3. a model function; and
4. a vector of initial guesses for the parameters.

Independent variable and observations

Power spectrum of x-axis QPD voltage. 3.2 μm silica spheres trapped with 80 mW laser power. Sampling frequency was 50 MHz.

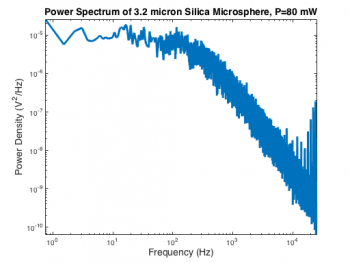
The second order system model of the optical trap makes predictions about the power spectrum of a thermally excited, trapped bead. The optical trap records a time sequence of voltages, not a power spectrum, so it is necessary to convert the raw data to a power spectrum for fitting. Frequency is known precisely, so it will serve as the independent variable in the regression. Power is the (noisy) dependent variable.

The MATLAB function pwelch computes a power spectrum $ P_{xx} $ and associated frequency bin vector $ f $ from a time series. Like many MATLAB functions, there are several different ways to invoke pwelch.The signatures of pwelch are particularly opaque — even by Mathworks' standards. Here is the command that generated the spectrum on the right:

[ Pxx, frequency ] = pwelch( OpticalTrapTimeDataX, [], [], [], 50000 );

The first argument, OpticalTrapTimeDataX is an Nx1 vector containing the QPD x-axis voltage samples. Empty values for the next three parameters (window, noverlap, and f) leave them set to their default values. The last argument to pwelch is the sampling frequency, $ f_s $. We will reexamine the default parameter settings later on.

Model function

nlinfit requires that the regression model be expressed as a function that takes two arguments and returns a single vector of predicted values. The signature of the function must look like this:

[ PredictedValues ] = ModelFunction( Beta, X ).

The first argument is a vector of model parameters. The second argument is a vector of independent variable values. The return value must must have the same size as the second argument.

The MATLAB function below implements a model of a second order system. There are three model parameters in the vector: undamped natural frequency, $ \omega_0 $, damping ratio $ \zeta $, and low-frequency power density $ P_0 $.

function [ PowerDensity ] = SecondOrderSystemPowerSpectrum( ModelParameters, Frequency )
    
    undampedNaturalFrequency = ModelParameters(1);
    dampingRatio = ModelParameters(2);
    dcGain = ModelParameters(3);

    s = 2i * pi * Frequency;

    response = dcGain * undampedNaturalFrequency.^2 ./ ...
        ( s.^2 + 2 * undampedNaturalFrequency * dampingRatio * s + undampedNaturalFrequency.^2 );
    
    PowerDensity = abs( response ).^2;

end

First attempt

Range of independent variable

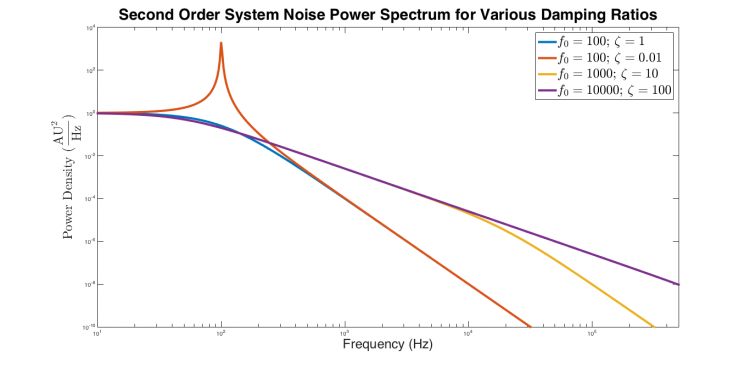
Power spectra of critically damped, underdamped, and overdamped second order systems excited by white noise. The underdamped response is flat at low frequencies, exhibits a narrow peak near $ f_0 $, and decreases with slope -4 at high frequencies. The critically damped response is flat from low frequency until approximately $ f_0 $, after which it falls with a slope of -4. Both overdamped systems are flat at low frequencies. They decrease with slope -2 at intermediate frequencies from approximately $ \frac{f_0}{\zeta} $ to $ f_0 $, after which the response decreases with slope -4.