Difference between revisions of "Estimating second order system parameters from noise power spectra using nonlinear regression"
(→Overview) |
(→Overview) |
||
| Line 35: | Line 35: | ||
--> | --> | ||
==Overview== | ==Overview== | ||
| − | In the limits of detection lab, you will use nonlinear regression to estimate the parameters of second-order systems that model the behavior of optical traps and atomic force microscopes. Nonlinear regression has a lot in common with chainsaws. In skilled hands, both <tt>nlinfit</tt> and a [http://www.stihlusa.com/products/chain-saws/professional-saws/ms880r/ 9 horsepower Stihl Magnum] are productive, accurate power tools that deliver and sublime results with a minimum of effort<ref>See, for example, [http://www.chainsawking.com/burton-and-lucas-films-collaborate-on-new-snowboard-park-at-sierra-resort/107_3063/] or [http://www.chainsaw-art.com/]</ref>. But great power comes with great danger. | + | In the limits of detection lab, you will use nonlinear regression to estimate the parameters of second-order systems that model the behavior of optical traps and atomic force microscopes. Nonlinear regression has a lot in common with chainsaws. In skilled hands, both <tt>nlinfit</tt> and a [http://www.stihlusa.com/products/chain-saws/professional-saws/ms880r/ 9 horsepower Stihl Magnum] are productive, accurate power tools that deliver and sublime results with a minimum of effort<ref>See, for example, [http://www.chainsawking.com/burton-and-lucas-films-collaborate-on-new-snowboard-park-at-sierra-resort/107_3063/] or [http://www.chainsaw-art.com/]</ref>. But great power comes with great danger. Both of these formidable tools must be used with extraordinary care. Inattentive or unskilled operation engenders distorted, ugly, or even catastrophic<ref>Do not follow this link if you are at all squeamish: [https://www.toolbox.co.uk/chainsaw-injuries]</ref> outcomes. |
An important difference between chainsaws and <tt>nlinfit</tt> is that chainsaw accidents are almost always graphic and obvious, whereas many grave regression wounds are stealthy. Bad regressions can easily masquerade as good ones — concealing their insidious flaws behind an alluring, plausible pair of overlapping curves. Because of this, it especially important to maintain a critical and alert mindset in the vicinity of regression. After every regression, do the responsible thing: spend some time ascertaining how disgraceful the sin you just committed was. | An important difference between chainsaws and <tt>nlinfit</tt> is that chainsaw accidents are almost always graphic and obvious, whereas many grave regression wounds are stealthy. Bad regressions can easily masquerade as good ones — concealing their insidious flaws behind an alluring, plausible pair of overlapping curves. Because of this, it especially important to maintain a critical and alert mindset in the vicinity of regression. After every regression, do the responsible thing: spend some time ascertaining how disgraceful the sin you just committed was. | ||
Revision as of 14:43, 28 June 2015
… the safe use of regression requires a good deal of thought and a good dose of skepticism
If your program generates an error message rather than curve fitting results, you probably won’t be able to make sense of the exact wording of the message.
—Motulsky and Shristopoulos. Fitting Models to Biological Data using Linear and Nonlinear Regression
You won't find a tool with more power per inch than a chain saw. Power like that requires extra attention to safety.
—lowes.com
Overview
In the limits of detection lab, you will use nonlinear regression to estimate the parameters of second-order systems that model the behavior of optical traps and atomic force microscopes. Nonlinear regression has a lot in common with chainsaws. In skilled hands, both nlinfit and a 9 horsepower Stihl Magnum are productive, accurate power tools that deliver and sublime results with a minimum of effort[1]. But great power comes with great danger. Both of these formidable tools must be used with extraordinary care. Inattentive or unskilled operation engenders distorted, ugly, or even catastrophic[2] outcomes.
An important difference between chainsaws and nlinfit is that chainsaw accidents are almost always graphic and obvious, whereas many grave regression wounds are stealthy. Bad regressions can easily masquerade as good ones — concealing their insidious flaws behind an alluring, plausible pair of overlapping curves. Because of this, it especially important to maintain a critical and alert mindset in the vicinity of regression. After every regression, do the responsible thing: spend some time ascertaining how disgraceful the sin you just committed was.
This page offers some advice that will help you retain all of your digits and limbs as you regress power spectra from the AFM and optical trap. Several flawed regressions are illustrated, followed by possible fixes. This sort of thing frequently happens in the development of a good regression: it takes a few tries to get the kinks out. Along the way, there are many signs of possible problems. Unfortunately, there are no definitive indicators of success. It can be difficult to tell when it's safe to stop.
Regression concepts review
Nonlinear regression is a method for finding the relationship between a dependent variable $ y_n $ and an independent variable $ x_n $. The two quantities are related by a model function $ f(\beta, x_n) $. $ \beta $ is a vector of model parameters. The dependent variable $ y_n $ is measured in the presence of random noise, which is represented mathematically by a random variable $ \epsilon_n $. In equation form:
- $ y_n=f(\beta, x_n)+\epsilon_n $.
The goal of regression is to determine a set of best-fit model parameters $ \hat{\beta} $ that match the observed data as closely as possible. Because the dependent variable includes noise, $ \hat{\beta} $ will not be equal to $ \beta $. As you can probably guess, decreasing the noise or increasing the number of observations tends to give a more reliable estimate.
Ordinary nonlinear least squares regression assumes that:
- the independent variable is known exactly, with zero noise,
- the error values are independent and identically distributed,
- the distribution of the error terms has a mean value of zero,
- the independent variable covers a range adequate to define all the model parameters, and
- the model function exactly relates $ x $ and $ y $.
These assumptions are almost never perfectly met in practice. It is important to consider how badly the regression assumptions have been violated when assessing results.
Get ready …
You need four things to run a regression:
- a vector containing the values of the independent variable;
- a vector containing the corresponding observed values of the dependent variable;
- a model function; and
- a vector of initial guesses for the model parameters.
Independent variable and observations
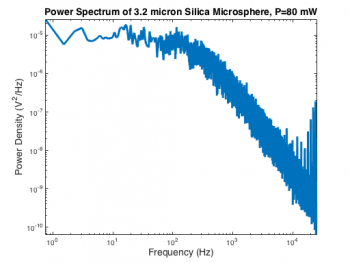
The second order system model of the optical trap makes predictions about the power spectrum of a thermally excited, trapped microsphere, whereas the instrument actually records a time sequence of voltages from the QPD position detector. The raw data must be converted into a power spectrum before fitting.
MATLAB has a function called pwelch that computes a power spectrum $ P_{xx}(f) $ and associated frequency bin vector $ f $ from a time series. Like many MATLAB functions, there are several different ways to invoke pwelch. Even judging by Mathworks' low standards for clarity and consistency, the various forms of pwelch are perplexing. Here is the command that generated the spectrum on the right:
[ Pxx, frequency ] = pwelch( OpticalTrapTimeDataX, [], [], [], 50000 );
The first argument, OpticalTrapTimeDataX is an Nx1 vector containing the QPD x-axis voltage samples. Empty values for the next three parameters (window, noverlap, and f) leave them set to their default values. The last argument is the sampling frequency, $ f_s $. We will reexamine the default parameter settings later on.
The two quantities in the regression are frequency and power spectral density. One of these has to serve as the independent variable, and the other as dependent. To make the best choice, consider the relative influence of measurement noise on each quantity. The optical trap has a very accurate and precise oscillator circuit that generates its sample clock. Because the sample frequency is so stable, measurement error in the frequency values calculated by pwelch is tiny. Power spectral density, on the other hand, is inherently noisy due to the random nature of the thermal driving force. You can see how wiggly the power spectrum is in the vertical direction. So the choice of independent and dependent variables is easy: the low-noise quantity, frequency, will serve as the independent variable and the noisy quantity, power spectral density, will be the dependent variable.
Model function
nlinfit requires that the regression model be expressed as a function that takes two arguments and returns a single vector of predicted values. The signature of the model function must must have the form:
[ PredictedValues ] = ModelFunction( Beta, X ).
The first argument, Beta, is a vector of model parameters. The second argument, X is a vector of independent variable values. The return value, PredictedValues, must must have the same size as X.
The MATLAB function defined below models the power spectrum of a second-order system excited by white noise. The three model parameters are passed to the function in a 1x3 vector: undamped natural frequency $ f_0 $, damping ratio $ \zeta $, and low-frequency power density $ P_0 $.
function [ PowerDensity ] = SecondOrderSystemPowerSpectrum( ModelParameters, Frequency )
undampedNaturalFrequency = 2 * pi * ModelParameters(1);
dampingRatio = ModelParameters(2);
lowFrequencyPowerDensity = ModelParameters(3);
s = 2i * pi * Frequency;
response = lowFrequencyPowerDensity * undampedNaturalFrequency.^2 ./ ...
( s.^2 + 2 * undampedNaturalFrequency * dampingRatio * s + undampedNaturalFrequency.^2 );
PowerDensity = abs( response ).^2;
end
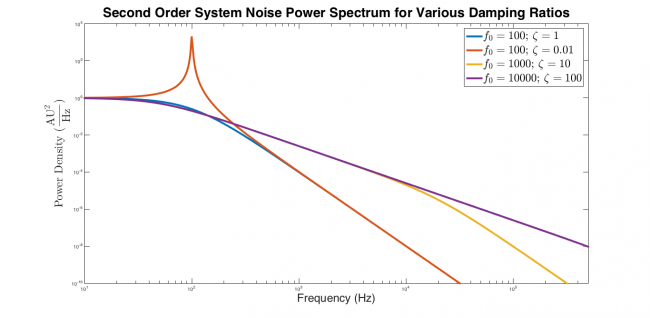
It's a good idea to test the model function out before you use it. The plot below shows four sets of curves generated by SecondOrderSystemPowerSpectrum. The critically damped response is flat from low frequency until approximately $ f_0 $, after which it falls with a slope of -4. The underdamped response exhibits a narrow peak near $ f_0 $ and then decreases with slope -4 at high frequencies. Both overdamped systems are flat at low frequencies. They decrease with slope -2 at intermediate frequencies from approximately $ \frac{f_0}{\zeta} $ to $ f_0 $, after which the response falls with slope -4. It's comforting to see that the curves have the expected shape.
Initial guesses
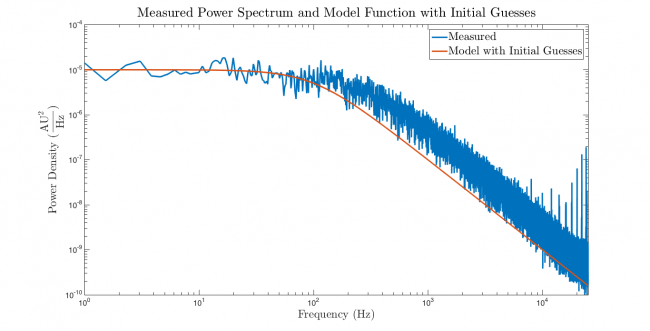
There are three model parameters, so three initial guesses are required. nlinfit infers the number of model parameters from the size of the Initial guess vector. Accordingly, the initial guesses should be stored in a 1x3 vector. You can eyeball a reasonable starting point by taking a look at the PSD plot, say: 500 Hz for $ f_0 $, 10-5 AU2/Hz for $ P_0 $, and 1 for the damping ratio.
Get set …
The first step of all regressions is to plot the observations and the model function evaluated with the initial guesses versus the independent variable on a single set of axes. Don't attempt to run nlinfit until you've done this plot. It is much easier to ensure that the arguments to nlinfit are in order before you invoke it than to debug a screen full of cryptic, red text after. Side effects of premature regression include confusion, waste of time, fatigue, irritability, alopecia, and feelings of frustration. There is no chance that nlinfit will succeed if there is a problem with one of its arguments.
Go ahead ... do the plot.
Now we can proceed with confidence that the arguments to nlinfit are plausible.
Go ... first attempt
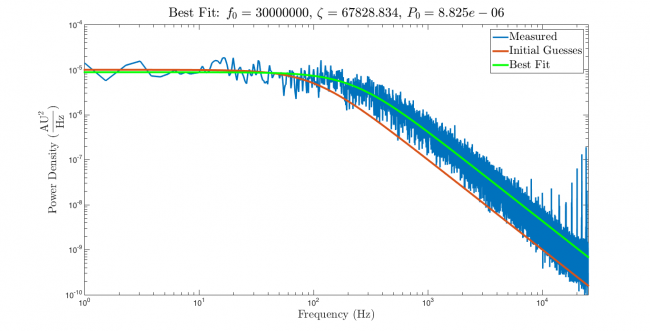
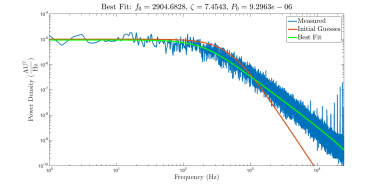
The plot below shows the results of running regression with the data, model, and initial guesses developed so far. The green line on the plot shows the model function evaluated with best-fit parameters $ \hat{\beta} $. The best-fit model nicely overlaps the measured data.
Success! Great curves!
Not so fast. If you let the alluring, overlapping blue and green curves in the plot above get you excited, go back and reread this page from the beginning. Much more scrutiny is required. On top of the usual reasons to be skeptical, an additional cause for concern materialized in the console output window. MATLAB barfed up a long, impenetrable, word salad of foreboding red verbiage. Running the regression triggered two different warnings.
The first warning repeated itself about a dozen times, each time with a slightly different value of "tol":
Warning: Rank deficient, rank = 2, tol = 1.099158e-10. > In nlinfit>LMfit (line 574) In nlinfit (line 276)
Then the regression finished with a second distress signal:
Warning: Some columns of the Jacobian are effectively zero at the solution, indicating that the model is insensitive to some of its parameters. That may be because those parameters are not present in the model, or otherwise do not affect the predicted values. It may also be due to numerical underflow in the model function, which can sometimes be avoided by choosing better initial parameter values, or by rescaling or recentering. Parameter estimates may be unreliable. > In nlinfit (line 373)
The first warning is terse and cryptic. The second one is spectacularly ambiguous. It's impossible to know how to react. Deep concern? Annoyance? Fear? Rage? Apathy? (It's just a warning, after all.) The parameter estimates MAY be unreliable. But then again they MAY not. A more forthright author could have written, "This regression smells fishy. Almost anything could have caused the problem. Beware."
So is this regression a good one or a bad one? Red text spewing from nlinfit is never good news, but It is sometimes not bad news. How can you tell? When it comes to error messages and warnings, nlinfit works just like the Mystic Seer that featured prominently in the unforgettable 43rd Twilight Zone episode Nick of Time starring William Shatner as a superstitious newlywed with car trouble stranded in a small town and Patricia Breslin as his beautiful and sensible bride[3]. Over-interpreting the willfully vague pronouncements of a mechanical contrivance is a path to subjugation and doom. The real enemy is within.
Or is there perhaps a greater force at play? It's best not to spend too much time figuring it out. Get out of town while you still can.
Assessing the regression results 1: examine the residuals
With some effort, It's possible to decode the warning messages generated by the previous regression. (This page has a good discussion of rank deficiency.) But even if you understand the warnings perfectly, there is still a long list of root problems might have led to either of the warnings. nlinfit can detect concerning symptoms, but it doesn't have the ability to suss their implications. So the warning messages tend to either avoids the issue (as in the first warning) or produce a laundry list of possibilities (as in the second warning). This is probably why nlinfit and the Mystic Seer seem to have so much in common.
Instead of trying to decipher the warning messages, it's frequently more productive to revisit the construction of the regression. Violations of the regression assumptions are a leading cause of trouble. One of the most fundamental assumptions in the regression model is that the error terms are independent and identically distributed. An easy way to gauge the validity of this assumption is to plot the vector of residuals versus the independent variable and have a look. (The second value returned from nlinfit contains a vector of the residuals.) If the regression assumptions are perfectly met, the plot should look something like the plot on the left below. The plot below on the right shows the actual residuals from this regression.
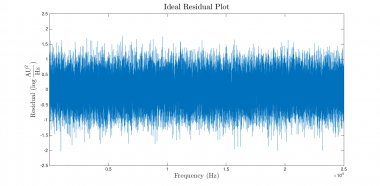 |
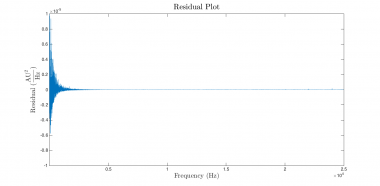
|
Holey moley! The right plot does not look at all like the left one. The magnitude of the residuals decreases dramatically as frequency increases — a significant and unacceptable violation of the regression assumptions. We definitely have a bad regression on our hands.
This has to be fixed before moving on.
Second attempt
In retrospect, the problem with the residuals in the first regression should have been obvious. A quick glance at the PSD plot reveals that the measurement error (fuzziness of the line) is about the same size over the entire range of the plot. But the axes are scaled logarithmically, so a certain level of fuzziness near the top of the plot represents a much larger measurement error than the same amount of fuzziness near the bottom of the plot. The errors are nowhere near identically distributed, so there wan't any hope of getting a good residual plot. It turns out that the measurement error in the PSD is roughly proportional to the magnitude squared of the instrument's transfer function.
Why does the measurement error in the PSD scale that way? Handwaving alert: the following explanation is not particularly rigorous. At a fundamental level, measuring the power of a signal in a certain frequency band is similar to measuring the average weight of a grain of sand on all the beaches of the world. It's not practical to measure every single grain of sand. The next best thing is to measure a random sample and use the mean weight of the sample as a proxy for the true answer. Unfortunately, no matter how carefully you choose the subpopulation of sand grains to measure, it will not be perfectly representative. Just by luck of the draw, a particular random sample will be lighter or heavier than the average. The sample mean weight will differ from the true mean weight.
Signals extend over an infinite time period, so It's even less practical to measure an entire signal than every grain of sand. It's possible to estimate a power spectrum using a similar approach, though: measure a representative sample and use that as a proxy. For a power spectrum, the representative sample is a finite time interval of time. Just by chance, the signal will have a little more power than usual at some frequencies and a little less at others during the measurement window. This manifests as uncertainty or variation in the PSD measurement. For example, if you could somehow measure the spectrum of white noise over an infinite time period, it would be perfectly flat line — exactly equal magnitude at all frequencies. The PSD of a white noise signal measured over a finite time interval looks like a fuzzy, horizontal line.The details of the fuzziness in the finite-time power spectrum estimate are different every time you repeat the measurement.
The model of the optical trap is a second-order system driven by white (thermal) noise. The output of the position detector is measured over a finite time window. Over the measurement window, the input signal's power spectrum is not perfectly representative — it's a fuzzy line. The output PSD is equal to the input PSD multiplied by the magnitude squared of the transfer function. So both the average value and the fuzziness in the input power spectrum get scaled. Assuming the uncertainty in the input signal's power spectrum has the same distribution at all frequencies, the measurement error in the output power spectrum is proportional to the magnitude squared of the transfer function. (If you are interested in a more mathematically precise argument, this presentation is a good starting point)
- $ y_n = f(\beta,x_n) + \epsilon_n f(\beta,x_n) = f(\beta,x_n) ( 1 + \epsilon_n ) $
Fortunately, there are a few easy ways to fix the problem. One approach is to transform the dataset into log space[4]:
- $ \log{y_n}=\log{f(\beta,x_n) ( 1 + \epsilon_n )}=\log{f(\beta,x_n)}+log{[1+\epsilon_n ]} $
Taking the log of the dependent variable turns multiplicative noise into additive noise. The code below uses MATLAB's anonymous function syntax to create a log-space version of the model function.
logModelFunction = @( p, f ) log( SecondOrderSystemPowerSpectrum( p, f ) );
Simple enough. Now call nlinfit with logModelFunction instead of @ModelFunction. Remember to also take the log of $ P_{xx} $.
Here are the results and the new residual plot:
 |
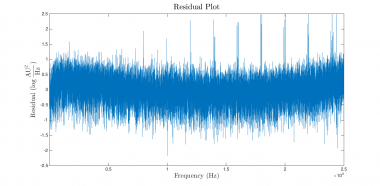
|
The estimate of $ f_0 $ changed by more than 250 Hz, and the residual plot is much closer to the ideal. Progress.
There is a slight smile shape to the curve that indicates the presence of systematic error in the model. (In other words, the model function does not perfectly match the system — perhaps due to nonlinearity.) But the distribution of the residuals looks a great deal more like the ideal plot and the deviation from the model is small.
MATLAB's warning this time is much shorter (but not more helpful):
Warning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit (line 376)
In general, the less red text produced by nlinfit the better.
Assessing the regression 2: parameter confidence intervals
Let's continue with the strategy of ignoring the details of the warning message for a little bit longer and move on to the next step of assessing the regression results.
Parameter confidence intervals are a measure of uncertainty in the best-fit parameter values, $ \hat{\beta} $. Confidence intervals are always expressed with an associated level of uncertainty, usually a percentage. (The default confidence level is 95% if you use the MATLAB function nlparci to compute parameter confidence intervals.) Conceptually, you can think of a 95% parameter confidence interval like this: Imagine that you repeated the measurement procedure precisely the same way 100 times. Because of random noise alone, the values of $ \hat{\beta} $ would be a little different for each trial (assuming all the sources of systematic error were also identical). $ \hat{\beta} $ would fall within the confidence interval 95 times of of the 100 trials.
Large parameter confidence intervals can be a sign of trouble. Small intervals are a good sign, but they do not a guarantee that a regression was correct. Freakin' regression.
Computing the parameter confidence intervals is easy in MATLAB:
[bestFit, residuals, jacobian,covariance,mse] = ...
nlinfit( f, log( Pxx ), logModelFunction, initialGuesses );
parameterConfidenceIntervals = nlparci( bestFit, residuals, 'covar', covariance );
Here are the 95% confidence intervals for the current regression returned by nlparci.
| Parameter | Upper Bound | Lower Bound | Units |
|---|---|---|---|
| $ f_0 $ | 2904.702141 | 2904.702146 | Hz |
| $ \zeta $ | 7.27 | 7.64 | (unitless) |
| $ P_0 $ | 8.89 | 9.70 | $ \frac{\text{V}^2}{\text{Hz}} $ |
So is this good or bad news? The confidence intervals are not immediately unnerving. (Confidence intervals that include zero are a sure sign of trouble.) It's interesting that the interval for $ f_0 $ is unbelievably small and the ones for $ \zeta $ and $ P_0 $ are much larger.
Third attempt
The warning about the ill-conditioned Jacobian implies that a small change in the observations could bring about a large change in $ \hat{\beta} $, which is not too comforting. There are two knees in the second-order, overdamped PSD curve (that is, two places where the slope changes). At large damping ratios, the second knee occurs at a much higher frequency than the first knee. The theoretical value of the damping ratio for the optical trap is equal to $ \frac{3 \pi \eta D}{\sqrt(k m)} $. Order of magnitude, this is probably more than 102 and maybe even greater than 103, depending on the size of the bead and the laser power setting. The first knee is around 100 Hz, so that puts the second knee at 10 MHz, which is very far above the highest frequency in the PSD, 25 KHz. Large changes in the damping ratio make only inconsequential changes in the low-frequency power spectrum. As such, the range of frequency values measured is not large enough to assure a good value for $ \zeta $
Comparing the three regressions
- ↑ See, for example, [1] or [2]
- ↑ Do not follow this link if you are at all squeamish: [3]
- ↑ If you haven't seen this sublime 25 minutes of televised perfection, go watch it right now. I will give a 24 hour extension to anybody who writes a 1-5 page essay on the episode.
- ↑ Two other reasonable approaches to fixing the problem are: change the value of the ErrorModel parameter to nlinfit, or use the Weights option.