|
|
| Line 104: |
Line 104: |
| | * Sketch V<sub>neuron</sub> and V<sub>scope</sub> assuming that V<sub>neuron</sub> is a 1 ms duration, square pulse of magnitude 100 mV. You may neglect the oscilloscope's resistance in this part of the problem. | | * Sketch V<sub>neuron</sub> and V<sub>scope</sub> assuming that V<sub>neuron</sub> is a 1 ms duration, square pulse of magnitude 100 mV. You may neglect the oscilloscope's resistance in this part of the problem. |
| | * How many times does the student curse during the measurement attempt? | | * How many times does the student curse during the measurement attempt? |
| − | * Ignoring capacitance, what is the minimum input impedance that a measurement device must have in order to make a high-fidelity measurement of an action potential. | + | * Ignoring capacitance, what is the minimum input impedance that a measurement device must have in order to make a high-fidelity measurement of an action potential? |
| | }} | | }} |
| | | | |
| | | | |
| | {{Template:20.309 bottom}} | | {{Template:20.309 bottom}} |
Revision as of 13:43, 19 October 2018
20.309: Biological Instrumentation and Measurement

This is Part 2 of Assignment 6.
Ideal elements

|
For each of the ideal, two-terminal elements listed below, show the symbol, label the terminals, indicate the direction of current flow, write the constitutive equation, and find an expression for the impedance, $ Z(\omega)=\frac{V}{I} $. (To find the impedance, substitute $ V=Ae^{j\omega t} $ into the constitutive equation and solve for $ \frac{V}{I} $ as a function of $ \omega $.)
- Resistor
- Capacitor
- Inductor
- Voltage source
- Current source
|
Resistive circuits

|
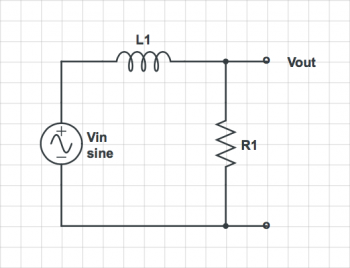
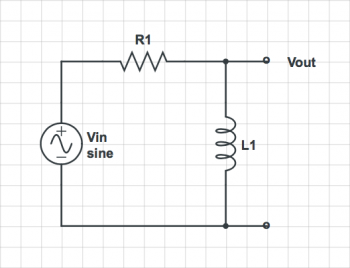
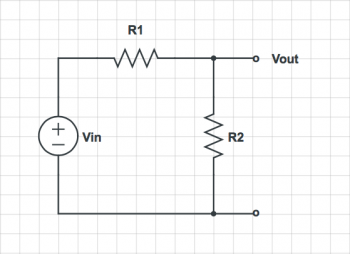
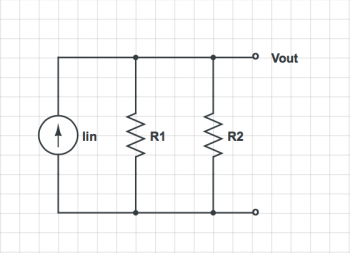
For each of the circuits below, find the voltage at each node and the current through each element.
|
| 1
|
2
|
|
|
| 3
|

Equivalent circuits

|
For each of the circuits in the previous problem, find two equivalent circuits — the first one consisting of a single voltage source and a single resistor, and the second one consisting of one current source and one resistor. In both equivalent circuits, the I-V curve at the Vout the port should be identical to the original circuit.
|
Easy Bode plots

|
For each of the circuits below, find the transfer function $ H(\omega)=\frac{V_{out}}{V_{in}} $. On a log-log plot, sketch the magnitude of the transfer function versus frequency. Sketch the phase angle of the transfer function versus frequency on a semi-log plot. Suggest a descriptive name for each circuit (e.g. "low-pass filter.")
|
Harder Bode plots

|
For each of the circuits below, find the transfer function $ H(\omega)=\frac{V_{out}}{V_{in}} $.
Simplify the transfer functions using the following assumptions:
- For the first circuit, assume that $ R_1 C_1 \gg R_2 C_2 $, and $ R_2 \gg R_1 $
- For the second circuit, assume that $ R_1 C_1 = R_2 C_2 $, and $ R_2 \gg R_1 $
On a log-log plot, sketch the magnitude of the simplified transfer function versus frequency. Label cutoff frequencies. Sketch the phase angle of the transfer function versus frequency on a semi-log plot. Suggest a descriptive name for each circuit.
|
| 1
|
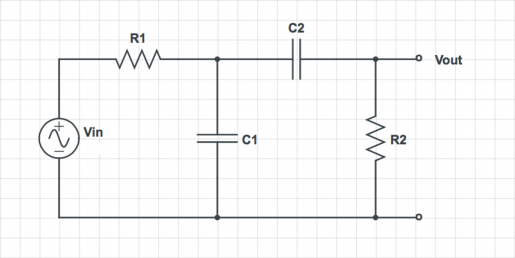
|
| 2
|
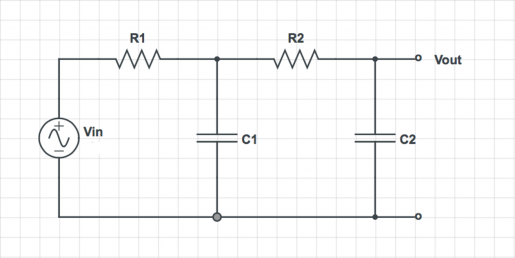
|
Linear systems

|
Assuming R1 = 1 Ω and C1 = 1 μFd, find an equation for $ V_{out}(t) $ for each circuit given the following inputs:
- $ v_{in}(t)=cos( 2 \pi * 0.1 t ) + cos( 2 \pi * 10 * t ) $
- $ v_{in}(t)=cos( 2 \pi t ) $
- $ v_{in}(t)=cos( 2 \pi * 10^{-6} t ) + cos( 2 \pi * 10^6 * t ) $
Feel free to make reasonable approximations. You should only get an urge to use a calculator for the first one.
|
| 1
|
2
|
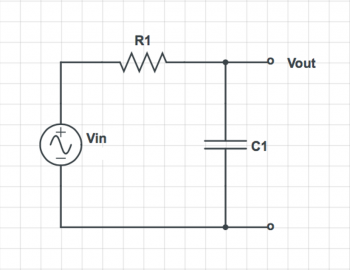
|

|
Measuring action potentials
The patch clamp is a technique for measuring voltages produced by electrically active cells such as neurons. A circuit model for a neuron connected to a patch clamp apparatus consists of a time-varying voltage source in series with an output impedance of 1011 Ω. There is an oscilloscope next to the neuron with an input impedance of 106 Ω and an input capacitance of 20 pFd. A new UROP in the lab attempts to measure the electrical spikes produced by a neuron (called action potentials) by connecting the patch clamp apparatus to the oscilloscope with a cable that has a capacitance of 80 pFd. Action potentials are about 100 mV in amplitude and about 1 ms in duration. The oscilloscope has a noise floor of 10-3 V.


|
- Neglecting the cable and oscilloscope capacitance, what is the magnitude of Vscope, the signal the student measures, after connecting the oscilloscope?
- Is the measurement successful? Why or why not?
- What is the signal to noise power ratio $ \left( \frac{V_{patch}}{V_{noise}} \right )^2 $ of the measurement (neglecting the capacitance)?
- Sketch Vneuron and Vscope assuming that Vneuron is a 1 ms duration, square pulse of magnitude 100 mV. You may neglect the oscilloscope's resistance in this part of the problem.
- How many times does the student curse during the measurement attempt?
- Ignoring capacitance, what is the minimum input impedance that a measurement device must have in order to make a high-fidelity measurement of an action potential?
|
|