Electronics bootcamp II: feedback systems
From Course Wiki
Revision as of 19:23, 29 October 2018 by MAXINE JONAS (Talk | contribs)
--Steven Wasserman (talk) 21:14, 27 October 2018 (CDT)
Time and frequency response of a feedback system
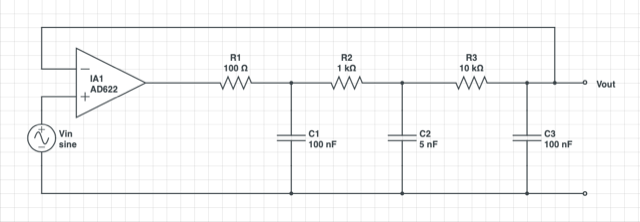
In the second part of the boot camp, you will build the circuit below and characterize its time and frequency response.
| Overdamped | Critically damped |
|---|---|

|
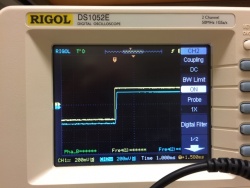
|
| Slightly underdamped | Underdamped |
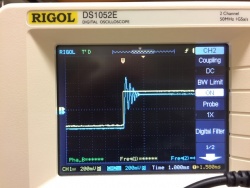
|
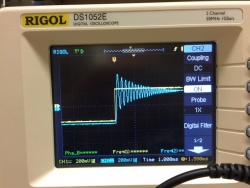
|
- Find the transfer function of the RC network inside the feedback loop (not including the amplifier). Use an appropriate approximation to dramatically simplify the algebra.
- Find the transfer function of the entire system, including the amplifier, as a function of the amplifier's open-loop gain, A.
- Build and test the circuit in the diagram.
- Connect the output of a signal generator to channel 1 of an oscilloscope and also to the input of your circuit.
- Connect the output of your circuit to channel 2 of the oscilloscope.
- Set the function generator to produce a 100 Hz, square wave output with an amplitude of 100 mV.
- Adjust Rgain (between pins 1 and 8 of the AD622 instrumentation amplifier) so that the system response is slightly overdamped.
- Measure the frequency response of the system as you did in part 1 of the electronics bootcamp (Assignment 6).
- Find the transfer function, the undamped natural frequency, and the damping coefficient.
- Plot the data and transfer function (as you did in part 1)
- Adjust Rgain so that the circuit is critically damped and repeat steps 6-8.
- To achieve critical damping, start with an over damped response and vary Rgain by turning the potentiometer until there is a slight overshoot in the response. Then turn the potentiometer back until the overshoot just disappears.
- Adjust Rgain so that the circuit is slightly underdamped (two or three overshoots) and repeat steps 6-8.
- Adjust Rgain so that the circuit is underdamped with at least a dozen or so overshoots and repeat steps 6-8.