Capacitors and inductors

Capacitors

A capacitor is a device that stores energy in an electric field which is generated by equal and opposite electric charge on opposing electrodes or plates within the capacitor. In turn, the charge Q is proportional to the voltage across the capacitor,

$ Q = CV\frac{}{} $

where C is the capacitance (units of farads (F) ≡ coulombs/volt). The current through the capacitor is the time rate of change of the charge and so the terminal relation of voltage and current for a capacitor is

$ i_C(t) = \frac{dQ}{dt} = C \frac{dV_C}{dt} $

R-C circuit driven by a step voltage V₀.

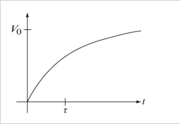
In an R-C circuit where a capacitor is charged via a current-limiting resistor from a step voltage source V₀ (the voltage is zero for t<0 and V₀ for t>0),

$ i = \frac{V_0-V_C}{R} = C \frac{dV_C}{dt} $

for t>0, or

$ V_0-V_C = RC \frac{dV}{dt} $

This first-order differential equation has the well-known solution

$ V_C(t) = A e^{-t/\tau} + B\frac{}{} $

Transient step voltage response of R-C circuit.

where τ=RC is the "RC" time constant. At time t=0 there is no charge or voltage on the capacitor so V_C(0)=0 and A=−B. Also as t→∞ then V_C→B a constant and so i→0 and the voltage across the resistor also goes to zero. We conclude that B=V₀ and, therefore,

$ V_C(t) = V_0 (1-e^{-t/\tau})\frac{}{} $

Inductors

In contrast to a capacitor, an inductor is a device that generates and stores energy in a magnetic field internally. In turn, the time rate of change of this magnetic field generates a voltage (Faraday's law of induction),

$ V_L(t) = L \frac{di_L}{dt} $

where L is the inductance (units of henrys (H) ≡ volt⋅second/ampere). For a constant current, the voltage across the inductor is identically zero.

L-R circuit driven by a step voltage V₀.

In an L-R circuit where an inductor is driven in series with a current-limiting resistor from a step voltage source V₀,

$ V_L = L \frac{di_L}{dt} = V_0 - i_L R $

for t>0, or

$ \frac{L}{R} \frac{di_L}{dt} = \frac{V_0}{R} - i_L $

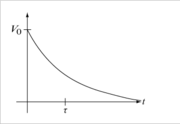
This is almost identical to the case of the R-C circuit above, except here we are solving for the current through the inductor instead of voltage. Here we make the same arguments about the inductor current as we did for the capacitor voltage, that is, at time t=0 we must have i_L=0 and as t→∞ then i_L→V₀/R. Therefore,

$ i_L(t) = \frac{V_0}{R} (1-e^{-t/\tau}) $

Transient step response of L-R circuit.

where now τ=L/R is the "L over R" time constant. The inductor voltage may be found simply by taking the derivative of the current,

$ v_L(t) = L \frac{V_0}{R} \frac{d}{dt}(1-e^{-t/\tau}) = V_0 \frac{L}{R}\frac{1}{\tau}e^{-t/\tau} = V_0 e^{-t/\tau} $