Difference between revisions of "Capacitors and inductors"
Eliot Frank (Talk | contribs) |
Eliot Frank (Talk | contribs) |
||
| Line 2: | Line 2: | ||
A capacitor is a device that stores energy in an electric field which is generated by equal and opposite electric charge on opposing electrodes or plates within the capacitor. In turn, the charge ''Q'' is proportional to the voltage across the capacitor, | A capacitor is a device that stores energy in an electric field which is generated by equal and opposite electric charge on opposing electrodes or plates within the capacitor. In turn, the charge ''Q'' is proportional to the voltage across the capacitor, | ||
| − | <math>Q = CV\frac{}{}</math> | + | : <math>Q = CV\frac{}{}</math> |
where ''C'' is the capacitance (units of farads (F) ≡ coulombs/volt). The current through the capacitor is the time rate of change of the charge and so the terminal relation of voltage and current for a capacitor is | where ''C'' is the capacitance (units of farads (F) ≡ coulombs/volt). The current through the capacitor is the time rate of change of the charge and so the terminal relation of voltage and current for a capacitor is | ||
| − | <math>i_C(t) = \frac{dQ}{dt} = C \frac{dV_C}{dt}</math> | + | : <math>i_C(t) = \frac{dQ}{dt} = C \frac{dV_C}{dt}</math> |
[[Image:ElectronicsModuleFig-RC.png|thumb|right|R-C circuit driven by a step voltage ''V<sub>0</sub>''.]] | [[Image:ElectronicsModuleFig-RC.png|thumb|right|R-C circuit driven by a step voltage ''V<sub>0</sub>''.]] | ||
| − | In an R-C circuit where a capacitor is charged via a current-limiting resistor from a step voltage source ''V<sub>0</sub>'' (the voltage is zero for ''t<0'' and ''V<sub>0</sub>'' for ''t>0''), | + | In an R-C circuit where a capacitor is charged via a current-limiting resistor from a step voltage source ''V<sub>0</sub>'' (the voltage is zero for ''t<0'' and ''V<sub>0</sub>'' for ''t>0''), the current through the resistor is identical to the current through the capacitor. The resistor current is found simply by taking the voltage drop across the resistor divided by ''R'', |
| − | <math>i = \frac{V_0-V_C}{R} = C \frac{dV_C}{dt}</math> | + | : <math>i = \frac{V_0-V_C}{R} = C \frac{dV_C}{dt}</math> |
| − | for ''t>0'' | + | for ''t>0''. This equation may be rewritten in terms of voltages as |
| − | <math>V_0-V_C = RC \frac{ | + | : <math>V_0-V_C = RC \frac{dV_C}{dt}</math> |
This first-order differential equation has the well-known solution | This first-order differential equation has the well-known solution | ||
| − | <math>V_C(t) = A e^{-t/\tau} + B\frac{}{}</math> | + | : <math>V_C(t) = A e^{-t/\tau} + B\frac{}{}</math> |
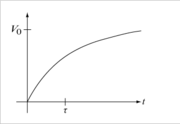
[[Image:ElectronicsModuleFig-exp-rising.png|thumb|right|Transient step voltage response of R-C circuit.]] | [[Image:ElectronicsModuleFig-exp-rising.png|thumb|right|Transient step voltage response of R-C circuit.]] | ||
where ''τ=RC'' is the "RC" time constant. At time ''t=0'' there is no charge or voltage on the capacitor so ''V<sub>C</sub>(0)=0'' and ''A=−B''. Also as ''t→∞'' then ''V<sub>C</sub>→B'' a constant and so ''i→0'' and the voltage across the resistor also goes to zero. We conclude that ''B=V<sub>0</sub>'' and, therefore, | where ''τ=RC'' is the "RC" time constant. At time ''t=0'' there is no charge or voltage on the capacitor so ''V<sub>C</sub>(0)=0'' and ''A=−B''. Also as ''t→∞'' then ''V<sub>C</sub>→B'' a constant and so ''i→0'' and the voltage across the resistor also goes to zero. We conclude that ''B=V<sub>0</sub>'' and, therefore, | ||
| − | <math>V_C(t) = V_0 (1-e^{-t/\tau})\frac{}{}</math> | + | : <math>V_C(t) = V_0 (1-e^{-t/\tau})\frac{}{}</math> |
| Line 31: | Line 31: | ||
In contrast to a capacitor, an inductor is a device that generates and stores energy in a magnetic field internally. In turn, the time rate of change of this magnetic field generates a voltage (Faraday's law of induction), | In contrast to a capacitor, an inductor is a device that generates and stores energy in a magnetic field internally. In turn, the time rate of change of this magnetic field generates a voltage (Faraday's law of induction), | ||
| − | <math>V_L(t) = L \frac{di_L}{dt}</math> | + | : <math>V_L(t) = L \frac{di_L}{dt}</math> |
where ''L'' is the inductance (units of henrys (H) ≡ volt⋅second/ampere). For a constant current, the voltage across the inductor is identically zero. | where ''L'' is the inductance (units of henrys (H) ≡ volt⋅second/ampere). For a constant current, the voltage across the inductor is identically zero. | ||
| Line 38: | Line 38: | ||
In an L-R circuit where an inductor is driven in series with a current-limiting resistor from a step voltage source ''V<sub>0</sub>'', | In an L-R circuit where an inductor is driven in series with a current-limiting resistor from a step voltage source ''V<sub>0</sub>'', | ||
| − | <math>V_L = L \frac{di_L}{dt} = V_0 - i_L R</math> | + | : <math>V_L = L \frac{di_L}{dt} = V_0 - i_L R</math> |
for ''t>0'', or | for ''t>0'', or | ||
| − | <math>\frac{L}{R} \frac{di_L}{dt} = \frac{V_0}{R} - i_L</math> | + | : <math>\frac{L}{R} \frac{di_L}{dt} = \frac{V_0}{R} - i_L</math> |
This is almost identical to the case of the R-C circuit above, except here we are solving for the current through the inductor instead of voltage. Here we make the same arguments about the inductor current as we did for the capacitor voltage, that is, at time ''t=0'' we must have ''i<sub>L</sub>=0'' and as ''t→∞'' then ''i<sub>L</sub>→V<sub>0</sub>/R''. Therefore, | This is almost identical to the case of the R-C circuit above, except here we are solving for the current through the inductor instead of voltage. Here we make the same arguments about the inductor current as we did for the capacitor voltage, that is, at time ''t=0'' we must have ''i<sub>L</sub>=0'' and as ''t→∞'' then ''i<sub>L</sub>→V<sub>0</sub>/R''. Therefore, | ||
| − | <math>i_L(t) = \frac{V_0}{R} (1-e^{-t/\tau})</math> | + | : <math>i_L(t) = \frac{V_0}{R} (1-e^{-t/\tau})</math> |
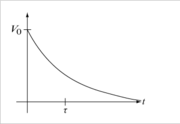
[[Image:ElectronicsModuleFig-exp-falling.png|thumb|right|Transient step response of L-R circuit.]] | [[Image:ElectronicsModuleFig-exp-falling.png|thumb|right|Transient step response of L-R circuit.]] | ||
where now ''τ=L/R'' is the "L over R" time constant. The inductor voltage may be found simply by taking the derivative of the current, | where now ''τ=L/R'' is the "L over R" time constant. The inductor voltage may be found simply by taking the derivative of the current, | ||
| − | <math>v_L(t) = L \frac{V_0}{R} \frac{d}{dt}(1-e^{-t/\tau}) | + | : <math>v_L(t) = L \frac{V_0}{R} \frac{d}{dt}(1-e^{-t/\tau}) |
= V_0 \frac{L}{R}\frac{1}{\tau}e^{-t/\tau} = V_0 e^{-t/\tau} </math> | = V_0 \frac{L}{R}\frac{1}{\tau}e^{-t/\tau} = V_0 e^{-t/\tau} </math> | ||
Revision as of 14:42, 25 March 2013
Capacitors
A capacitor is a device that stores energy in an electric field which is generated by equal and opposite electric charge on opposing electrodes or plates within the capacitor. In turn, the charge Q is proportional to the voltage across the capacitor,
- $ Q = CV\frac{}{} $
where C is the capacitance (units of farads (F) ≡ coulombs/volt). The current through the capacitor is the time rate of change of the charge and so the terminal relation of voltage and current for a capacitor is
- $ i_C(t) = \frac{dQ}{dt} = C \frac{dV_C}{dt} $
In an R-C circuit where a capacitor is charged via a current-limiting resistor from a step voltage source V0 (the voltage is zero for t<0 and V0 for t>0), the current through the resistor is identical to the current through the capacitor. The resistor current is found simply by taking the voltage drop across the resistor divided by R,
- $ i = \frac{V_0-V_C}{R} = C \frac{dV_C}{dt} $
for t>0. This equation may be rewritten in terms of voltages as
- $ V_0-V_C = RC \frac{dV_C}{dt} $
This first-order differential equation has the well-known solution
- $ V_C(t) = A e^{-t/\tau} + B\frac{}{} $
where τ=RC is the "RC" time constant. At time t=0 there is no charge or voltage on the capacitor so VC(0)=0 and A=−B. Also as t→∞ then VC→B a constant and so i→0 and the voltage across the resistor also goes to zero. We conclude that B=V0 and, therefore,
- $ V_C(t) = V_0 (1-e^{-t/\tau})\frac{}{} $
Inductors
In contrast to a capacitor, an inductor is a device that generates and stores energy in a magnetic field internally. In turn, the time rate of change of this magnetic field generates a voltage (Faraday's law of induction),
- $ V_L(t) = L \frac{di_L}{dt} $
where L is the inductance (units of henrys (H) ≡ volt⋅second/ampere). For a constant current, the voltage across the inductor is identically zero.
In an L-R circuit where an inductor is driven in series with a current-limiting resistor from a step voltage source V0,
- $ V_L = L \frac{di_L}{dt} = V_0 - i_L R $
for t>0, or
- $ \frac{L}{R} \frac{di_L}{dt} = \frac{V_0}{R} - i_L $
This is almost identical to the case of the R-C circuit above, except here we are solving for the current through the inductor instead of voltage. Here we make the same arguments about the inductor current as we did for the capacitor voltage, that is, at time t=0 we must have iL=0 and as t→∞ then iL→V0/R. Therefore,
- $ i_L(t) = \frac{V_0}{R} (1-e^{-t/\tau}) $
where now τ=L/R is the "L over R" time constant. The inductor voltage may be found simply by taking the derivative of the current,
- $ v_L(t) = L \frac{V_0}{R} \frac{d}{dt}(1-e^{-t/\tau}) = V_0 \frac{L}{R}\frac{1}{\tau}e^{-t/\tau} = V_0 e^{-t/\tau} $