Difference between revisions of "Bode plots and frequency response"

From Course Wiki
Jump to: navigation, search
Line 4: Line 4:
  
 
One way to visualize a transfer function is to make two plots. The first plot shows the gain verses frequency on a set of log-log axes. The second plot shows the phase shift versus log frequency.
 
One way to visualize a transfer function is to make two plots. The first plot shows the gain verses frequency on a set of log-log axes. The second plot shows the phase shift versus log frequency.
−
 
−
A Bode plot is a log-log representation plot of the magnitude of a transfer function versus frequency.  In a Bode plot, only straight line segments are used to approximate the transfer function.  At a critical or cutoff frequency, there is an abrupt change in slope in the transfer function instead of a smooth transition (e.g., from pass band to stop band).
 
  
 
[[Image:ElectronicsModuleFig-RC.png|thumb|right|First-order R-C low-pass filter.]]
 
[[Image:ElectronicsModuleFig-RC.png|thumb|right|First-order R-C low-pass filter.]]
Line 11: Line 9:
  
 
: <math> H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi f RC} </math>
 
: <math> H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi f RC} </math>
 +
In this case the cutoff frequency is given by <math>f_C = 1 / (2\pi RC) </math>.
  
−
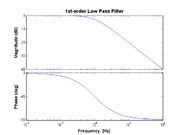
In this case the cutoff frequency is given by <math>f_C = 1/(2\pi RC)</math>.  In the Bode plot of this function, a straight line segment with zero slope for <math>f < f_C</math> represents the pass band of the filter while a line with a slope of &minus;1 for <math>f > f_C</math> represents the stop band.
 
  
−
[[Image:BodePlot-LowPass.png|thumb|right|Bode plot of low-pass transfer function.]]
+
[[Image:BodePlot-LowPass.png|thumb|right|Bode plot of low-pass filter with cutoff frequency <math> f_C=1 </math>.]]
  
 
More examples
 
More examples
  
 +
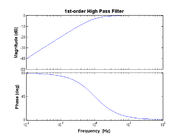
[[Image:BodePlot-HighPass.png|thumb|right|Bode plot of high-pass transfer function  with cutoff frequency <math> f_{HP}=1 </math>.]]
 
High-pass
 
High-pass
  
−
: <math> H(f) = \frac{j2\pi f \tau_{\rm HP}}{1 + j2\pi f \tau_{\rm HP}} </math>
 
 
: <math> H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} </math>
 
: <math> H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} </math>
  
 +
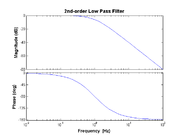
[[Image:BodePlot-SecondOrder.png|thumb|right|Second order low-pass transfer function. Note that the scale of the plots are double that of the 1st-order filter.]]
 
Second-order low-pass
 
Second-order low-pass
  
−
: <math> H(f) = \left(\frac{1}{1 + j2\pi f \tau_{\rm LP}}\right)^2 </math>
 
 
: <math> H(f) = \left(\frac{1}{1 + j f / f_{\rm LP}}\right)^2 </math>
 
: <math> H(f) = \left(\frac{1}{1 + j f / f_{\rm LP}}\right)^2 </math>
  
 +
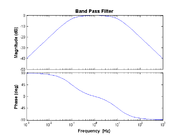
[[Image:BodePlot-BandPass.png|thumb|right|Frequency response of band-pass transfer function with <math> f_{HP}=0.1 </math> and <math> f_{LP}=10 </math>.]]
 
Band pass
 
Band pass
  
−
: <math> H(f) = \frac{j2\pi f \tau_{\rm HP}}{1 + j2\pi f \tau_{\rm HP}}
 
−
    \times \frac{1}{1 + j2\pi f \tau_{\rm LP}} </math>
 
 
: <math> H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}}  
 
: <math> H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}}  
 
     \times \frac{1}{1 + j f / f_{\rm LP}} </math>
 
     \times \frac{1}{1 + j f / f_{\rm LP}} </math>
  
 
{{Template:20.309 bottom}}
 
{{Template:20.309 bottom}}

Revision as of 14:39, 3 April 2013

20.309: Biological Instrumentation and Measurement

ImageBar 774.jpg

Overview

Only two things can happen to a sine wave passing through a linear, time-invariant system: it's magnitude can be changed; and the signal can be delayed. The delay and percentage change in the magnitude are a function of frequency. A transfer function, H(f), is a complex-valued function of frequency that specifies the magnitude and phase shift of a particular system for all frequencies. The change in amplitude is often called the gain, and the delay is usually thought of in terms of a phase shift of the sine wave.

One way to visualize a transfer function is to make two plots. The first plot shows the gain verses frequency on a set of log-log axes. The second plot shows the phase shift versus log frequency.

First-order R-C low-pass filter.

For example, consider a simple RC low-pass filter with the transfer function is given by

$ H(f) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j2\pi f RC} $

In this case the cutoff frequency is given by $ f_C = 1 / (2\pi RC) $.


Bode plot of low-pass filter with cutoff frequency $ f_C=1 $.

More examples

Bode plot of high-pass transfer function with cutoff frequency $ f_{HP}=1 $.

High-pass

$ H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} $
Second order low-pass transfer function. Note that the scale of the plots are double that of the 1st-order filter.

Second-order low-pass

$ H(f) = \left(\frac{1}{1 + j f / f_{\rm LP}}\right)^2 $
Frequency response of band-pass transfer function with $ f_{HP}=0.1 $ and $ f_{LP}=10 $.

Band pass

$ H(f) = \frac{j f / f_{\rm HP}}{1 + j f / f_{\rm HP}} \times \frac{1}{1 + j f / f_{\rm LP}} $
Retrieved from "http://engineerbiology.org/w/index.php?title=Bode_plots_and_frequency_response&oldid=6871"