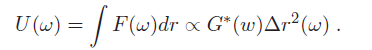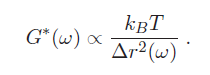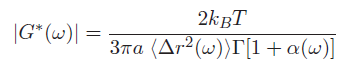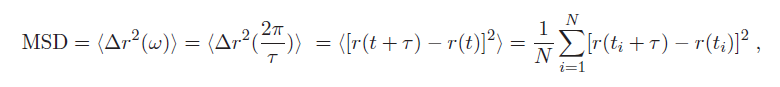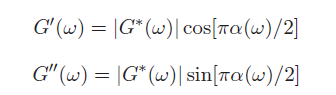Difference between revisions of "Optical Microscopy Part 4: Particle Tracking"

Introduction and Background

Many cellular functions such as migration, differentiation, and proliferation are regulated by the mechanical properties of cells, specifically, their elasticity and viscosity. Rheology is the science of measuring materials' mechanical properties. Microrheology is a subgroup of techniques that are capable of measuring mechanical properties from microscopic material volumes. Clearly, given the typical size of biological cells, microrheology is the technique needed to measure their elasticity and viscosity. The elastic and viscous properties of cells can be characterized by a complex-valued shear modulus (with units of Pa) G*(ω) = G'(ω) + iG"(ω). The real part G'(ω), referred to as the storage modulus, is a measure of cell elasticity, while the imaginary part G"(ω), the loss modulus, is a measure of their viscosity. A generalized Hookian relationship can be written as:

where Δr is a generalized displacement, and F(ω) is a force linearly proportional to it via the shear modulus. Therefore, we can measure the shear modulus if we can measure the deformation of the cell under a known force. (Note that all these quantities are frequency-dependent). Particle-tracking microrheometry is based on measuring the displacement of a particle with radius a embedded in a cell driven by thermal forces. One complication is that this relationship is frequency dependent - this is because in complex fluids, such as the cellular cytoskeleton, there are different energy dissipation mechanisms over different time scales. To approach the derivation of the relevant formulas, it is more convenient to think in terms of energy, rather than force. The relationship between stored energy and displacement has a familiar form, similar to a spring-mass system (recall $ KE \ \alpha \ k(\omega)^2 $):

What is the driving thermal energy U(ω)? Recall also that thermal energy is "white," i.e., it contains equal power at all frequencies and is equal to 0.5*k$ _B $T for each degree of freedom in a second-order system, where k$ _B $ is Boltzmann's constant and T is the absolute temperature. From this relationship (since we're observing motion in two dimensions), we have

Our argument is clearly very rough but a complete (and much more difficult) derivation results in the following equation (see Mason ^[1] for details):

$ \left\vert G^*(\omega) \right\vert = {k_B T \over \pi a \left \langle \Delta r^2 (\omega) \right \rangle \Gamma[1 + \alpha(\omega)]} $

Some key additional details to help you make sense of this equation:

1. As you can see, the dependence on displacement is more accurately expressed as the mean- square displacement (MSD) <Δr$ ^2 $(ω)>:

where < > denotes a time-average of the particle's displacement trajectory r(t), at discrete times t = t$ _1 $,.... t$ _n $ (as sampled by a digital system like the PC and camera). Additionally, τ is a characteristic lag/delay time for the measurement. corresponding to the frequency ω.

2. $ \alpha(\omega)=\frac{\partial \ln \left \langle \Delta r^2(\tau) \right \rangle }{\partial \ln \tau} $

3. The radius of the particle a plays a role in the formula.

4. Γ(.) is the Gamma function (the generalized form of the factorial function, which can be looked up in a mathematical table). Mason suggests that for our range of α,

$ \Gamma[1 + \alpha] \approx = 0.457(1 + \alpha)^2 - 1.36(1 + \alpha) + 1.90. $

This equation may look complicated but there is a simple approximation to calculate the elastic and viscous moduli:

A detailed discussion of particle tracking microrheology can be found in the papers by Mason and Lau^[2] An application of the work of Mason et al to 3T3 cells in particular can be found in the work of Tseng et al. ^[3]

Experiment Details

Live Cell Measurements

After previously verifying that your system is sufficiently stable, you can run the experiment on cell samples. A key technique to keep in mind when working with live cells - to avoid shocking them with "cold" at 20°C, be sure that any solutions you add are pre-warmed to 37°C. We will keep a warm-water bath running for this purpose, in which we will keep the various media.

3T3 Swiss Albino

You are provided with NIH 3T3 fibroblasts, which were prepared as follows: Cells were cultured at 37°C in 5% CO$ _2 $ in standard T75 flasks in a medium referred to as DMEM++. This consists of DMEM (Invitrogen) supplemented with 10% fetal bovine serum (FBS - Invitrogen) and an antibiotic, 1% penicillin-streptomycin (Invitrogen). The day prior to the microrheology experiments, fibroblasts were plated on 35 mm glass-bottom cell culture dishes (MatTek). On the day of the experiments, the cell confluency should reach about 60%. 1 μm diameter orange fluorescent microspheres (Molecular Probes) were mixed with the growth medium (at a concentration of 5 x 10$ ^5 $ beads/mL) and added to the plated cells for a period of 12 to 24 hours for bead endocytosis.

1. Carefully pipet out the medium from both dishes. Replace with 2mL of fresh, pre-warmed medium in each dish.
2. Choose cells with 3 or 4 particles embedded in them and take a movie as before. Take multiple movies with about 3-5 cells in the field of view in each movie.
3. For one of the dishes, treat the cell with the cytoskeleton-modifying chemical cytochalasin D (CytoD): Pipet out the medium, add 1 mL CytoD solution at 10 μM (pre-mixed for you) to the dish, and wait for 20-30 min. It's a good idea to check on your cells after 20 min.: sometimes they are in bad shape at that point but sometimes they still look very healthy. Wash twice with 2mL pre-warmed DMEM++, leaving 2mL in the dish when imaging.
4. Repeat the particle tracking measurements again as quickly as you are able. Their physiology has now been significantly disrupted and they will die within a couple of hours. It's very unlikely that you'll be able to find the exact same cells you've already tracked; however it's very much advisable to use the same dish for the "before" and "after" so you're aren't also comparing between different cell populations.

References

1. ↑ T. G. Mason, "Estimating the viscoelastic moduli of complex fluids using the generalized Stokes-Einstein equation" Rheol. Acta, 39, pp. 371-378 (2000).
2. ↑ A. W. C. Lau et al., "Microrheology, Stress Fluctuations, and Active Behavior of Living Cells," Phys. Rev. Lett., 91(19), p. 198101 (2003)
3. ↑ Tseng et al. :Yiider Tseng, Thomas P Kole, and Denis Wirtz, "Micromechanical mapping of live cells by multiple-particle-tracking microrheology." Biophys J. 2002 December; 83(6): 3162–3176.