Error analysis
Warning: this page is a work in progress.
Overview
his page will help you understand and clearly communicate the causes and consequences of experimental error.
You will make quite a few measurements in 20.309. The purpose of making a measurement is to determine the value of some unknown physical quantity Q. In general, the measurement procedure you use will produce a measured value M that differs from Q by some amount E. Measurement error, E, is the difference between the true value Q and the measured value M, E = Q - M. People also use the terms observational error and experimental error to refer to E. Observational error causes uncertainty in a measurement.
Measurement error limits your ability to make inferences from experimental data. Your lab report must include a thorough, correct, and precise discussion of experimental errors and the effect they had on your data.
Many terms have special meanings in the context of error analysis. These key terms on this page are italicized when they are introduced.
Measurement quality
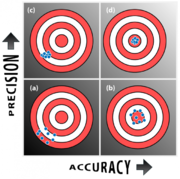
Measurements are characterized by their precision and accuracy. Precision encompasses errors that are random in nature. Accuracy comprises errors that are deterministic. Precision quantifies the variability of a measurement. Accuracy specifies how far a measurement is from the truth. (Because the term "accuracy" has been so poorly used, some people use the term "trueness" instead of accuracy.)
The total error in a measured quantity is equal to to the sum of the error contributions from all error sources. Each error source can be classified according to its variability. Random errors are unrepeatable fluctuations that reduce precision. Systematic errors are repeatable errors that reduce accuracy.
A pure random error can be modeled by a random variable that has some distribution with an average value μ = 0 and standard deviation σ. In the lab, you can get an estimate of σ by making several measurements of the same quantity and computing the sample standard deviation.
Pure systematic errors are deterministic functions of Q. A systematic error source always causes the same error E for a given value of Q. In the presence of a pure systematic error, repeated measurements of Q always give the same value. The standard deviation of a set of measurements that include a systematic error is zero. Therefore, multiple measurements do not reveal systematic errors, which makes systematic errors much more difficult to characterize than random errors. The principal way to detect a systematic error is to measure known standards. In many complex measurements, finding an appropriate standard is difficult.
Common models for systematic error sources include offset error (also called zero-point error), sensitivity error (also called percentage error), and nonlinearity. In a zero-point error, the observational error E is constant. If a standard is available, is possible to find the constant and subtract it from the result — a process called calibration. Sensitivity errors have the form E = K Q. Like offset errors, sensitivity errors can also be corrected by calibration (with at least two standards). In nonlinear errors, K is a function of Q. (The term "sensitivity" is frequently used imprecisely. It is probably clearer to call this type of error a responsivity error.) Nonlinear errors require a great deal more care to correct than offset and sensitivity errors.
Drift error is another fundamental kind of error that affects many measurements — particularly ones that are taken over long time intervals. Drift errors are systematic errors with a magnitude that changes over time. Temperature changes, humidity variations, and component aging are common sources of drift errors. Many drift errors have the characteristic that their magnitude increases roughly in proportion to the square root of time.
Most measurements include a combination of random, systematic, and drift errors. One kind of error frequently predominates.
Sources of error
Error sources are root causes of measurement errors. E is equal to the sum of the errors caused by each individual source. Some examples of error sources are: thermal noise, interference from other pieces of equipment, and miscalibrated instruments. Error sources fall into three categories: fundamental, technical, and illegitimate. Fundamental error sources are physical phenomena that place an absolute lower limit on experimental error. Fundamental errors cannot be reduced. (Inherent is a synonym for fundamental.) Technical error sources can (at least in theory) be reduced by improving the instrumentation or measurement procedure — a proposition that frequently involves spending money. Illegitimate errors are mistakes made by the experimenter that affect the results. There is no excuse for those, unless you were out quite late last night.
An ideal measurement is limited by fundamental error sources only.
Review of probability and statists concepts
This section is coming soon to a wiki page near you. Pay attention in lecture on 9/9.
Propagating errors
Measurements are frequently used as inputs to calculations. When calculating values based on measurements that include observational error, it is necessary to consider the effect of the error on the calculated value — a process called error propagation. A thorough treatment of error propagation would likely cause you to navigate away from this page to your favorite cat video. Fortunately, a few simply rules will get you through many of the calculations in 20.309. The treatment of errors in some analyses, like nonlinear regression, is more complicated.
This page has a concise summary of the rules for propagating errors through calculations. (Here is another succinct page.)
Averaging
One way to refine a measurement that exhibits random variation is to average N measurements:
- $ M=\frac{1}{N}\sum_{i=1}^{N}{M_i}=Q-\frac{1}{N}\sum_{i=1}^{N}{E_i} $
where Mi is the i th measurement and Ei is the i th measurement error, Ei = Q - Mi . Substituting Mi = Q + Ei into the summation reveals that the error terms Ei of multiple measurements average together. If the errors are random, the error terms tend to cancel each other.
The central limit theorem offers a good mathematical model for what happens when you average measurements that include random observational error. Informally stated, the theorem says that if you average N random variables that come from the same distribution with standard deviation σ, the standard deviation of the average will be approximately σ/√N. Averaging multiple measurements increases the precision of a result at the cost of decreased measurement bandwidth. In other words, you can't measure Q as frequently, which is a problem if you expect Q to be changing quickly. Precision comes at the expense of a longer measurement. The central limit theorem also says that if N is large enough, the distribution of the average will be approximately Gaussian. The central limit theorem holds under a wide range of assumptions about the distribution of the errors.
Averaging multiple measurements offers a simple way to increase the precision of a measurement. Because the precision increase is proportional to the square root of N, averaging is a resource intensive way to achieve precision. You have to average one hundred measurements to get a single additional significant digit in your result. The central limit theorem is your frenemy. The theorem offers an elegant model of the benefit of averaging multiple measurements. But it is also could also be called the Inherent Law of Diminishing Returns of the Universe. Each time you repeat a measurement, the incremental value added by your hard work diminishes. The tenth measurement is only about 11% as valuable as the first; the hundredth carries only about three percent of the benefit.
If it takes a long time to repeat a measurement for averaging, drift may become a significant factor.
Classifying errors

Classify error sources based on their type (fundamental, technical, or illegitimate) and the way they affect the measurement (systematic or random). In order to come up with the correct classification, you must think each source all the way through the system: how does the underlying physical phenomenon manifest itself in the final measurement? For example, many measurements are limited by random thermal fluctuations in the sample. It is possible to reduce thermal noise by cooling the experiment. Physicists cooled the pentacene molecules shown at right to 4°C in order to image them so majestically with an atomic force microscope. But not all measurements can be undertaken at such low temperatures. Intact biological samples do not fare well at 4°C. Thus, thermal noise could be considered a technical source in one instance (pentacene) and a fundamental source in another (most measurements of living biological samples). There is no hard and fast rule for classifying error sources. Consider each source carefully.
Example: the effect of a pill on temperature
Imagine you are conducting an experiment that requires you to swallow a pill and take your temperature every day for a month. You have two instruments available: an analog thermometer and a digital thermometer. Both thermometers came with detailed specifications.
The specification sheet for the analog thermometer says that it may have an offset error of up to 2°C and a random error of zero. (If you ever find a real thermometer with these specifications, be wary.) Assume you don't have a temperature standard you can use to find the value of the offset.
The manufacturer's website for the digital thermometer says that it has 0°C offset, but noise in its amplifier causes the reading to vary randomly around the true value. The variation has an approximately Gaussian distribution with an average value of 0°C and a standard deviation of 2°C.
Which thermometer should you use?
It depends.
The raw temperature data from the digital and analog thermometers could be used in a variety of ways. It is easy to imagine experimental hypotheses that involve the average, change in, or variance in your temperature. The two thermometers result in different kinds of errors in each of the three circumstances.
Bottom line: the magnitude of random errors tends to decrease with larger N; the magnitude of systematic errors does not.
If you are measuring your body mass index, which is equal to your mass in kilograms divided by your height in meters squared, your result M will be smaller than the true value Q. Your result will also include random variation from other sources. Averaging multiple measurements will reduce the contribution of random errors, but the measured value of BMI will still be too low. No amount of averaging will correct the problem.
Sample bias
Quantization error
Questions
Question 1
In the third century BCE, Eratosthenes measured E, the circumference of the Earth using only a stick, a piece of useful information, a few assumptions, and perhaps some camels. Unfortunately, many the details of Eratosthenes' method — like how he measured the distance between between Alexandriya and Syene — are lost to history. Scientific license and camels have been used to fill in some details for purposes of this question. For a thorough discussion and a lot of storytelling, see, for example: Circumference: Eratosthenes and the Ancient Quest to Measure the Globe by Nicholas Nicastro. Eratosthenes' measurement was certainly very accurate for its time, but since he used the archaic, non standardized units of stadia, nobody can be sure how close he was.
The piece of information Eratosthenes used was this: at noon on the day of summer solstice, in the city of Syene to the south of Alexandria where Eratosthenes lived, the sun shone on the bottom of a deep well and cast no shadow. Eratosthenes realized this meant that the sun was directly over Syene. At the same time in Alexandria, there were shadows. Eratosthenes measured the angle of the shadows in Alexandria at noon on the same day. You might presume that Eratosthenes used trigonometry to find E from the angle and the distance between the cities (assuming the Earth is a sphere). But trigonometry had not yet been invented. So instead, he determined what fraction of a circle the angle was (perhaps using a dividing compass) and set up a ratio:
Assume that Eratosthenes measured the distance between the two cities by timing how long it took several camels to make the voyage.
Question 2
Why should you be suspicious of a thermometer that specifies zero random error?
References
- ↑ Gross, et. al The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science 28 August 2009. DOI: 10.1126/science.1176210.