Assignment 2 Part 1: Noise in images

Overview

The process of recording a digital image is essentially an exercise in measuring the intensity of light at numerous points on a grid. Like most physical measurements, imaging is subject to measurement error. The formula below is a mathematical model of the imaging process, including noise and the camera's gain constant:

$ P_{x,y} =G \left( I_{x,y} + \epsilon_{x,y} \right) $,

where $ x $ and $ y $ are spatial coordinates, $ P_{x,y} $ is the matrix of pixel values returned by the camera , $ G $ is the gain of the camera, $ I_{x,y} $ is the actual light intensity in the plane of the detector, and $ \epsilon_{x,y} $ is a matrix of error terms that represent noise introduced in the imaging process.

Count von Count counting electrons.

The amount of information in any signal, such as an image or a neural recording or a stock price, depends on the Signal to Noise Ratio (SNR). In this part of the assignment, you will develop a software model for imaging noise sources and you will use your model to explore how different noise sources affect image SNR.

A (very) simplified model of digital image acquisition is shown in the image on the right. In the diagram, a luminous source stochastically emits $ \bar{N} $ photons per second. A fraction of the emitted photons lands on a semiconductor detector. Incident photons cause little balls (electrons) to fall out of the detector. The balls fall into a red bucket. At regular intervals, the bucket gets dumped out on to a table where the friendly muppet vampire Count von Count counts them. The process is repeated for each point on a grid. Not shown: the count is multiplied by a gain factor $ G $ before the array of measured values is returned to a recording device (such as a computer).

Before we dive into the computer model, it may be helpful to indulge in with a short review of (or introduction to) probability concepts.

Probability review

Random variable distributions

Plots of PDF $ f_x(x) $ vs. $ x $ and CDF $ F_x(x) $ vs $ x $ for the uniform distribution on the interval (0,1) and the normal distribution with $ \mu=0 $ and $ \sigma=1 $. MATLAB functions rand and randn return pseudorandom values that follow these distributions.

The question of what exactly a random variable is can get a bit philosophical. For present purposes, let's just say that a random variable represents the outcome of some stochastic process, and that you have no way to predict what the value of variable will be.

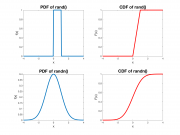
Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a Probability Density Function (PDF), usually written as $ f_x(x) $. Two commonly-used PDFs are shown in the plots on the right. Larger values of the PDF indicate more likely outcomes.

The probability that a continuous random variable will take on a particular value such as 0.5 is (perhaps counter-intuitively) zero. This is because there are an infinite number of possible outcomes. The chance of getting exactly 0.5 when there are an infinite set of possible outcomes is equal to one divided by infinity. In other words, there is no chance at all of getting exactly 0.5. This is kind of baffling to think about and certainly annoying to work with. It's frequently cleaner to work with intervals. The chance that a random variable will fall between two numbers $ a $ and $ b $ can be found by integrating the PDF from $ a $ to $ b $:

$ Pr(a \leq x \leq b)=\int_a^b f(x) $

The Cumulative Distribution Function $ F_x(x) $ is equal to the integral of the PDF from $ -\infty $ to $ x $:

$ F_x(x)=\int_{-\infty}^x f_x(\tau) d\tau $

$ F_x(x) $ is the probability that $ x $ takes on a value less than $ x $. Using the CDF, it easy to calculate probability that $ x $ falls within the interval $ [a,b] $:

$ Pr(a \leq x \leq b)=F_X(b)-F_x(a) $.

Mean, variance, and standard deviation

If you average a large number of outcomes of a random variable $ x $, the result approaches the variable's mean value $ \mu_x $:

$ \lim_{N\to\infty} \frac{1}{N} \sum_{1}^{N}{x_n}=\mu_x $

The mean can also be found from the PDF by integrating every possible outcome multiplied by its likelihood:

$ \mu_x=E(x)=\int_{−\infty}^{\infty}{x P(x) dx} $.

Standard deviation $ \sigma_x $ quantifies how far a random variable is likely to fall from its mean. Variance $ \sigma_x^2 $ is equal to the standard deviation squared. Sometimes, it is easier to work with variance in calculations. Most often, the interpretation of standard deviation is more intuitive than variance.

$ \sigma_x^2=\lim_{N\to\infty} \frac{1}{N} \sum_{1}^{N}{(x_n-\mu_x)^2} $

Variance can also be calculated from the PDF:

$ \sigma^2_x=\int_{−\infty}^{\infty}{(x-\mu)^2 P(x)dx} $

Calculations with random variables

If you add two random variables, their means add. Their variances also add. Standard deviations add under a big 'ol square root.

$ \mu_{x+y}=\mu_x+\mu_y $

$ \sigma_{x+y}^2=\sigma_x^2+\sigma_y^2 $

$ \sigma_{x+y}=\sqrt{\sigma_x^2+\sigma_y^2} $

Averaging

If you average N independent outcomes of a random variable, the standard deviation of the average is equal to

$ \sigma_{\bar{x},N}=\frac{\sigma_x}{\sqrt{N}} $

The standard deviation decreases in proportion to the square root of the number of averages. The term independent means that each outcome does not depend in any way on any other outcome.

Useful distributions

Binomial distribution

The binomial distribution considers the case where the outcome of a random variable is the sum of many individual go/no-go trials. The distribution assumes that the trials are independent and that the probability of success, $ p $, for each trial is the same. An example of a process that is well-modeled by the binomial distribution is the number of heads in 100 coin tosses. On each toss, the probability of success (heads) is $ p=0.5 $. If $ N $ is the number of trials, the average number of successes is equal to $ Np $. If you toss the coin 100 times, you expect on average to get 50 heads. The binomial distribution answers the question: "How surprised should I be if I get 12 heads?" The probability mass function (PMF) for a random variable x ~ B(N, p) gives the probability of getting exactly k successes in N trials:

$ Pr(k;n,p) = \Pr(x = k) = {n\choose k}p^k(1-p)^{n-k} $

for k = 0, 1, 2, ..., n, where

$ \binom n k =\frac{n!}{k!(n-k)!} $

(This is called a PMF instead of a PDF because it is discrete — you can only get an integer between 0 and N if when counting the number of successes in N trials.)

The standard deviation of a binomial distribution is:

$ \sigma_x^2=np(1-p) $

Poisson distribution

Sometimes, it is useful to model a binary process where you know the average value of the process, but not N and p. If p is small ($ p<<1 $), it is straightforward to make the approximation $ (1-p)=1 $. When p is small, a very good approximation of the variance is:

$ \sigma_x^2=np $

The variance of a Poisson-distributed variable is equal to its mean. The Poisson distribution is a useful model for photon emission, radioactive decay, the number of letters you receive in the mail, the number of page requests on a certain website, the number of people who get in line to check out at a store, and many other everyday situations. The ability to estimate the variability of a binary process without knowing N and p is incredibly useful.

Normal distribution. Each band has a width of 1 standard deviation

Normal distribution

The normal distribution (also frequently called a Gaussian distribution or a bell curve is specified by two parameters, an average value $ \mu $, and a standard deviation $ \sigma $:

$ f(x \; | \; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2} } \; e^{ -\frac{(x-\mu)^2}{2\sigma^2} } $

In the normal distribution, about 68% of outcomes fall within the interval $ \mu \pm \sigma $, about 95% in the interval $ \mu \pm 2 \sigma $, and about 99.7% in the interval $ \mu \pm 3 \sigma $

Central Limit Theorem

If you add together a bunch of independent random variables, their sum tends to look like a normal distribution

Modeling a single pixel

Let's start by modeling a single pixel. The first thing we need is a source of random numbers, so fire up MATLAB or any other computing you like on your computer (and stop whining about it). MATLAB includes several functions for generating random numbers. We will make our first model using the function rand(), which returns a random value that follows a uniform distribution in the interval (0, 1). Go ahead and type rand() at the command line. Matlab will return a number between 0 and 1. Do it a few times — it's kind of fun. You get a different number every single time. Can you guess what number will come next? If you can, please come see me.

If you want a bunch of random numbers, rand can help you out with that that, too. If you call rand with two integer M and N, the function will return a matrix of random numbers with M rows by N columns. The code snippet below to generates and displays (as an image) a 492 row x 656 column matrix of numbers with uniform distribution on the interval [0,1]:

noiseImage = rand( 492, 656 );
figure
imshow( noiseImage );

Now you know what what pure, uniformly-distributed noise looks like! In the Olden Days, when people used to watch things on analog television sets, it happened pretty frequently that the set would be tuned to a frequency where there was no station broadcasting. In a desperate attempt to find the signal, old-school television sets frantically turned up the gain on their internal amplifiers to the maximum. When this happened, tiny, electronic noise signals in the amplifier were amplified and displayed on the screen. You can simulate this pretty well in MATLAB:

figure
for ii = 1:100
    noiseImage = rand( 492, 656 );
    imshow( noiseImage )
    drawnow
end

This code snippet illustrates a couple of concepts you will find useful : how to code a for loop, and how to force a figure to update. The mysterious drawn command causes MATLAB to drop everything and finish all of its deferred tasks such as drawing on the screen. Tye leaving the drawnow out and see what happens. MATLAB decides that it has too much work to do to update the screen. If you want to make the simulation even better, add the command soundsc( randn( 1, 100000 ) ) to the beginning of your script.

Okay, enough goofing around with the random number generator. Assume you are imaging a single molecule has a 0.01% chance of emitting a photon per microsecond. For the time being, assume you have perfect detector with a 100% chance of detecting each photon. The exposure (duration over which the measurement is made) is 1 second. To model photon emission over a single microsecond, you can use the rand function like this: rand() < 0.0001. This statement will randomly return a value of 1 0.01% of the time and zero the rest of the time. On average, you would expect to detect about 100 photons during a one second long measurement. The simulation generates a million random numbers this way, and the sum function counts up the number of times a simulated photon is emitted.

close all
probabilityOfEmission = 1E-4;
numberOfPhotonsEmitted = zeros( 1, 100 );
for ii = 1:100
    numberOfPhotonsEmitted(ii) = sum( ( rand( 1, 1E6 ) < probabilityOfEmission ) );  % number of photons emitted
end

figure
plot( numberOfPhotonsEmitted, 'x' )
axis( [ 1 100 0 130 ] )
xlabel( 'n' )
ylabel( 'Number of Photons' )
title( 'Number of Photons Emitted (N=100 siumulations)' )

As you can see from the plot, just due to chance alone, the number of photons emitted is usually larger or smaller than 100. You can quantify the variation by computing the standard deviation of the results: type std( numbnerOfPhotonsEmitted )

Produce a log-log plot of standard deviation of the number of photons emitted as a function of the average number of photons emitted for probability of photon emission equal to the values: 1E-6, 1E-5, 1E-4, 1E-3, and 1E-2. Hint: use a nested loop. What is the relationship between the number of photons detected and the noise (standard deviation)? Repeat the simulation for an exposure time that is 100 X shorter and a light source that is 100 X more intense. Turn in the code you used to generate the plots

The uncertainty in light measurements that arises form the stochastic nature of photon emission is called shot noise.

Read noise and dark current noise

Johnson noise on an old, analog television set.

In addition to shot noise, the camera has some shortcomings that add to the noise in an image. In this section, you will add code to simulate these noise sources and redo the plots you did in the last section.

Even if the detector is in complete darkness, a few electrons still roll into the red bucket and they are counted by The Count just the same as the electrons that were generated by photons. This happens because the temperature of the detector is not at absolute zero. Just by chance there will be a few electrons with enough thermal energy to make it into the bucket. This is called dark current.

Another problem comes up when you try to count the electrons.

A few balls roll out of the detector and into the bucket and they are because a few electrons in the detector have high energy just by chance because the temperature of the detector is not zero.

Binomial and Poisson distributions

This kind of thing comes up quite a lot — where you have a bunch of identical events and each event either occurs or does not occur with a given probability $ p $. There is no possibility that the event half-occurs, so the event count will always take on an integer value. One of the best-known examples of this is a coin toss. Assuming the coin is fair, the probability of the event occurring (say, heads) $ p=0.5 $. If you flip a coin 100 times,

Referneces

• Overview
• Part 1: Noise in images
• Part 2: Fluorescence microscopy
• Part 3: Build an epi-illuminator for your microscope

Back to 20.309 Main Page