Assignment 2 Part 1: Noise in images

Overview

As you saw in Assignment 1, recording a digital image is essentially an exercise in measuring the intensity of light at numerous points on a grid. Stated mathematically, the task is to measure the spatially-varying magnitude of light intensity on a grid of points in a particular plane. The imaging process is subject to various noise sources. In this part of the lab, you will develop a software model for imaging noise sources and you will use it to explore how noise affects images. In particular, we will be asked to look into what factors determine the Signal to Noise Ratio (SNR) of an image. The amount of information in a signal (such an an image) depends on the SNR.

The figure on the right depicts a (very) simplified model of digital image acquisition. In the diagram, a luminous source stochastically emits $ \bar{N} $ photons per second. A fraction $ F_O $ of the emitted photons lands on a semiconductor detector. Incident photons cause little balls (electrons) to fall out of the detector. The balls fall into a red bucket. At regular intervals, the bucket gets dumped out on to a table where the friendly muppet vampire Count von Count counts them. The process is repeated for each point on a grid. Not shown: the count is multiplied by a gain factor $ G $ before the array of measured values is returned to a recording device (such as a computer).

The following formula represents the imaging process, including gain and noise:

$ P_{x,y} $=G \left I_{x,y} + \epsilon_{x,y} \right</math>,

where <$ x $ and $ y $ are spatial coordinates, $ P_{x,y} $ is the matrix of pixel values returned by the camera , $ G $ is the gain of the camera, $ I_{x,y} $ is the actual light intensity in the plane of the detector, and $ \epsilon_{x,y} $ is a matrix of error terms that represent noise introduced in the imaging process.

Before we go on to the computer model, it will be helpful to begin with a short review of (or introduction to) probability concepts.

Probability review

Modeling photon emission

Plots of PDF $ f_x(x) $ vs. $ x $ and CDF $ F_x(x) $ vs $ x $ for the uniform distribution on the interval (0,1) and the normal distribution with $ \mu=0 $ and $ \sigma=1 $. MATLAB functions rand and randn return pseudorandom values that follow these distributions.

In this part of the assignment, you will make a computer model of the process of measuring light in order to examine how noise sources affect images. Photon emission is a stochastic process, so we will start with a short review of (or introduction to) some probability concepts. The question of what exactly is a random variable can get a bit philosophical. For present purposes, let's just say that a random variable represents the outcome of some stochastic process, and that you have no way to predict what value that the variable will take.

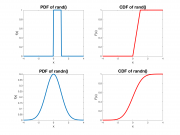
Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a Probability Density Function (PDF), usually written as $ f_x(x) $. Two commonly-used PDFs are shown in the plots on the right. Higher values indicate more likely outcomes.

The probability that a continuous random variable will take on a particular value like $ \pi $ or 0.5 is zero. This is because there are an infinite number of possible outcomes. The chance of getting one exact number out of an infinite set of possible outcomes is equal to one divided by infinity. In other words, there is no chance at all. This is kind of baffling to think about and certainly annoying to work with. It's usually easier to think about the chance that a variable will lie on an interval between two numbers $ a $ and $ b $. This can be found by integrating the PDF from $ a $ to $ b $:

$ Pr(a \leq x \leq b)=\int_a^b f(x) $

Since probability calculations so frequently use the integral of the PDF, whoever decides these things defined a function called the Cumulative Distribution Function $ F_X(x) $ that is equal to the integral of the PDF from $ -\infty $ to x:

$ F_x(x)=\int_{-\infty}^x f_x(x) $

$ F_x(x) $ is the probability that $ x $ takes on a value less than $ x $. The probability that $ x $ lies on the interval $ [a,b] $ is $ :Pr(a \leq x \leq b)=F_X(b)-F_x(a) $.

Two important properties of a PDF are its mean and standard deviation. Mean is a way to measure of the central tendency of a distribution and standard deviation is a measure of its spread. The mean is equal to the sum of every possible outcome times the probability of that outcome:

$ \mu=\int_{-\infty}^{\infty} x f(x) dx $.

Another way to think of the mean is like this: if you averaged lots of outcomes

It's time to fire up MATLAB. Feel free to use a another language, if you like. The commands are very similar in most languages.

We are going to model a stochastic process, so the first thing we need is a source of random numbers. MATLAB includes several functions for generating random numbers. We will to make our first model using the function rand(), which returns a random value that follows a uniform distribution in the interval (0, 1). Go ahead and type rand() at the command line. Matlab will return a number between 0 and 1. Do it a few times — it's kind of fun. Can you guess what number will come next? If you can, please come see me. If you want more than one random number, you can pass that information to rand with arguments. For example, try the code snippet below to generate and display (as an image) a matrix with 492 rows x 656 columns of numbers between 0 and 1:

totallyNoisyImage = rand( 492, 656 );
figure
imshow( totallyNoisyImage );

figure
hist( totallyNoiseImage(:) );

• Overview
• Part 1: Noise in images
• Part 2: Fluorescence microscopy
• Part 3: Build an epi-illuminator for your microscope

Back to 20.309 Main Page