Difference between revisions of "Assignment 2 Part 1: Noise in images"
(→Modeling photon emission) |
(→Modeling photon emission) |
||
| Line 14: | Line 14: | ||
==Modeling photon emission== | ==Modeling photon emission== | ||
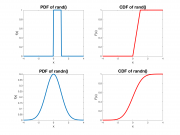
[[File:PDF and CDF of MATLAB rand and randn functions.png|thumb|right|Plots of PDF <math>f_x(x)</math> vs. <math>x</math> and CDF <math>F_x(x)</math> vs <math>x</math> for the uniform distribution on the interval (0,1) and the normal distribution with <math>\mu=0</math> and <math>\sigma=1</math>. MATLAB functions <tt>rand</tt> and <tt>randn</tt> return pseudorandom values that are drawn from these distributions.]] | [[File:PDF and CDF of MATLAB rand and randn functions.png|thumb|right|Plots of PDF <math>f_x(x)</math> vs. <math>x</math> and CDF <math>F_x(x)</math> vs <math>x</math> for the uniform distribution on the interval (0,1) and the normal distribution with <math>\mu=0</math> and <math>\sigma=1</math>. MATLAB functions <tt>rand</tt> and <tt>randn</tt> return pseudorandom values that are drawn from these distributions.]] | ||
| − | In this part of the assignment, you will make a computer model of the process of measuring light in order to examine how noise sources affect images. Photon emission is a stochastic process, so we will start with a short review of | + | In this part of the assignment, you will make a computer model of the process of measuring light in order to examine how noise sources affect images. Photon emission is a stochastic process, so we will start with a short review of probability concepts.The question of what exactly is a random variable is get a bit philosophical. For our present purposes, let's just say that a random variable represents the outcome of some a process, and that there is no way to predict the value that the variable will take. |
Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a ''Probability Density Function'' (''PDF''), usually written as <math>f_x(x)</math>. Two commonly-used PDFs are shown in the plots on the right. Higher values of the PDF indicate more likely outcomes. | Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a ''Probability Density Function'' (''PDF''), usually written as <math>f_x(x)</math>. Two commonly-used PDFs are shown in the plots on the right. Higher values of the PDF indicate more likely outcomes. | ||
Revision as of 17:46, 16 September 2017
Overview
Acquiring a digital image is essentially an exercise in measuring the intensity of light at numerous points on a grid. Light intensity measurements are subject to noise sources that limit the precision of images. In other words, when you try to measure how intense a light is, there will in general be a difference between the value that you measure and the true value of the light intensity. The difference between the measure value and the actual value quantities is called measurement error. Mathematically, measurement error can be modeled as a simple difference: $ M=Q+\epsilon $, where $ M $ is the measured value, $ Q $ is the true (unknowable) value of the quantity (light intensity in this case), and $ \epsilon $ is the measurement error. In this part of the assignment, you will develop a software model for the noise sources in a digital image and you will use it to explore how noise impacts digital images.
It turns out that the quantum nature of light has fundamental implications for the characteristics of noise in images. As such, we will measure light intensity in units of photons per second per area.
The figure on the right depicts a (very) simplified model of digital image acquisition. In the diagram, a luminous source stochastically emits $ \bar{N} $ photons per second. A fraction $ F_O $ of the emitted photons lands on a semiconductor detector. Incident photons cause little balls (electrons) to fall out of the detector. The balls fall into a red bucket. At regular intervals, the bucket gets dumped out on to a table where the friendly muppet vampire Count von Count counts them. The process is repeated for each point on a grid.
Modeling photon emission
In this part of the assignment, you will make a computer model of the process of measuring light in order to examine how noise sources affect images. Photon emission is a stochastic process, so we will start with a short review of probability concepts.The question of what exactly is a random variable is get a bit philosophical. For our present purposes, let's just say that a random variable represents the outcome of some a process, and that there is no way to predict the value that the variable will take.
Even though the value of a random variable is not predictable, it is usually the case that some outcomes are more likely than others. The specification of the relative likelihood of each outcome is called a Probability Density Function (PDF), usually written as $ f_x(x) $. Two commonly-used PDFs are shown in the plots on the right. Higher values of the PDF indicate more likely outcomes.
Unintuitively, the probability that a continuous random variable will take on a particular value like $ \pi $ or 0.5 is zero. This is because there are an infinite number of possible outcomes. The chance of getting one exact number out of an infinite set of possible outcomes is equal to one divided by infinity. In other words, there is no chance at all. This is kind of baffling to think about and certainly annoying to work with. It's usually easier to work out the chance that a variable will lie on an interval between two numbers $ a $ to $ b $. This can be found by integrating the PDF from $ a $ to $ b $:
- $ Pr(a<x<b)=\int_a^b f(x) $
Since probability calculations so frequently use the integral of the PDF, whoever decides these things decided to define a function called the Cumulative Distribution Function $ F_X(x) $ that is the integral of the PDF:
- $ F_x(x)=Pr[a \leq x \leq b]=\int_-\inf^b f_x(x) $
$ F_x(x) $ is the probability that $ x $ takes on a value less than $ x $. The probability that $ x $ lies on the interval $ \interval{a}{b} $, $ :Pr(\interval{a}{b})=F_X(b)-F_x(a) $.
In order to model a stochastic process, you need a source of random numbers. MATLAB includes several functions for generating random numbers.
rand() returns a random that has a uniform distribution in the interval (0, 1). Probabilistic distributions can be specified by , as shown on the right. The horizontal axis on the graph represents all the possible outcomes (real numbers), and the vertical axis represents the relative likelihood of a particular outcome. As shown in the graph, rand all numbers between 0 and 1 are equally likelyThe PDF of the distribution implemented by the rand function is shown on the right.
- Overview
- Part 1: Noise in images
- Part 2: Fluorescence microscopy
- Part 3: Build an epi-illuminator for your microscope
Back to 20.309 Main Page
- Overview
- Part 1: Noise in images
- Part 2: Fluorescence microscopy
- Part 3: Build an epi-illuminator for your microscope
Back to 20.309 Main Page </div>